


Next: As formas invariantes e
Up: Grupo de Lie
Previous: Grupo de Lie
(1)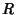 , com a operação de grupo tomada como sendo a
adição é um grupo de Lie.
, com a operação de grupo tomada como sendo a
adição é um grupo de Lie. 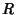 é uma variedade
diferenciável de dimensão 1, com um atlas formado por uma única
carta,
é uma variedade
diferenciável de dimensão 1, com um atlas formado por uma única
carta, 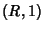 , onde
, onde 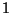 é a aplicação idêntica.
Algebricamente,
é a aplicação idêntica.
Algebricamente, 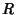 é um grupo, pois
é um grupo, pois
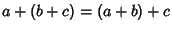 , a identidade
é
, a identidade
é 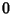 e o inverso de
e o inverso de 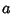 é
é 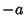 . Considere a operação
. Considere a operação
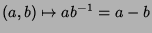 . Ela é obviamente uma operação
diferenciável de
. Ela é obviamente uma operação
diferenciável de
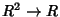 . Note que
. Note que 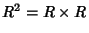 é
aqui a variedade produto
é
aqui a variedade produto 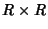 com um atlas
com um atlas
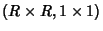 , onde
, onde
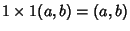 .
.
(2)Seja 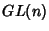 o conjunto das matrizes inversíveis
o conjunto das matrizes inversíveis 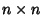 reais, com o produto de matrizes como multiplicação. O conjunto
das matrizes
reais, com o produto de matrizes como multiplicação. O conjunto
das matrizes 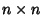 pode ser identificado com o
pode ser identificado com o 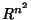 . O
. O
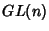 é um subconjuntode
é um subconjuntode 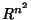 , caracterizado pelo seguinte:
se
, caracterizado pelo seguinte:
se 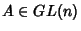 ,
, 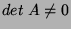 . É fácil mostrar que o conjunto
dos
. É fácil mostrar que o conjunto
dos 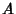 tais que
tais que 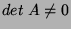 é um aberto de
é um aberto de 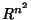 . Logo,
. Logo,
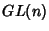 é uma subvariedade aberta de
é uma subvariedade aberta de 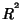 , e é, por conta
própria, uma variedade de dimensão
, e é, por conta
própria, uma variedade de dimensão 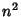 . A aplicação
. A aplicação
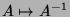 é diferenciável (Elon Lages lima, Curso de
Análise, Vol.2), bem como
é diferenciável (Elon Lages lima, Curso de
Análise, Vol.2), bem como
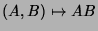 .
. 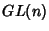 é, então,
um grupo de Lie.
é, então,
um grupo de Lie.
(3)A esfera 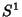 é um grupo de Lie; o toro
é um grupo de Lie; o toro
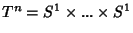 é um grupo de Lie.
é um grupo de Lie.
(4)O grupo 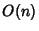 das matrizes ortogonais
das matrizes ortogonais 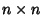 é um grupo de
Lie.
é um grupo de
Lie.



Next: As formas invariantes e
Up: Grupo de Lie
Previous: Grupo de Lie
Henrique Fleming
2001-12-26