


Next: About this document ...
Up: Grupos de Lie
Previous: As formas invariantes e
1. A variedade 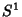 . Como conjunto,
. Como conjunto, 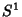 pode ser descrita como
pode ser descrita como
que é o círculo de raio 1 no plano complexo. Os pontos de 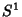 são os valores
de
são os valores
de 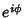 . Na figura vemos alguns desses pontos.
. Na figura vemos alguns desses pontos.
Tomemos a topologia induzida de 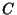 . Vamos mostrar que existe um sistema de cartas
que faz de
. Vamos mostrar que existe um sistema de cartas
que faz de 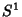 uma variedade diferenciável real de dimensão 1.
Considere a função
uma variedade diferenciável real de dimensão 1.
Considere a função
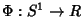 dada por
dada por
ou, equivalentemente,
A derivada de 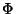 , dada por
, dada por
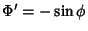 , anula-se para
, anula-se para
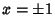 , o que significa que
, o que significa que 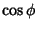 não tem inversa nesses pontos. Excluídos,
então,
não tem inversa nesses pontos. Excluídos,
então, 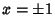 , a função
, a função
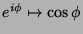 é um homeomorfismo
em um aberto de
é um homeomorfismo
em um aberto de 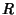 .
.
A função
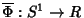 dada por
dada por
ou
tem o mesmo tipo de problema para 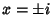 , pois aí se anula sua derivada.
Então, para pontos
, pois aí se anula sua derivada.
Então, para pontos 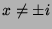 ,
,
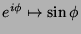 é um
homeomorfismo em um aberto de
é um
homeomorfismo em um aberto de 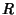 . Podemos então construir o seguinte atlas:
. Podemos então construir o seguinte atlas:
Para todo
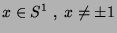 , tomamos a carta
, tomamos a carta 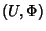 :
:
Para todo
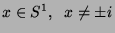 , tomamos a carta
, tomamos a carta 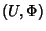 :
:
A compatibilidade é trivial. Suponhamos que, para o ponto 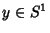 ,
valham as cartas
,
valham as cartas
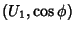 e
e
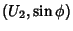 . Então, na
interseção
. Então, na
interseção 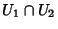 devemos ter
devemos ter
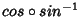 e
e
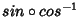 diferenciáveis. Mas,
diferenciáveis. Mas,
que é diferenciável.
2.O grupo de Lie 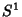
Se 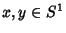 , a operação produto é
, a operação produto é
ou seja,
Para mostrar que ela é diferenciável, tomemos uma carta de
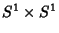 em torno de
em torno de
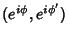 .
Suponhamos que a função seja o
.
Suponhamos que a função seja o 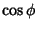 , e que a carta
seja
, e que a carta
seja
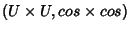 . Se
. Se
é a função multiplicação, sua representação local
é
que é uma função diferenciável de 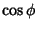 e de
e de
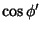 .
.
Portanto 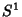 é um grupo de Lie real de dimensão 1.
é um grupo de Lie real de dimensão 1.



Next: About this document ...
Up: Grupos de Lie
Previous: As formas invariantes e
Henrique Fleming
2001-12-26
{$1$}
\uput[0](-0...
...$i$}
\uput[0](1.4,0.3){$-i$}
\psdots(2,0.5)(3.5,2)(2,3.5)(0.5,2)
\end{pspicture}](img190.png)
![]() dada por
dada por
![]() , tomamos a carta
, tomamos a carta ![]() :
:
![]() ,
valham as cartas
,
valham as cartas
![]() e
e
![]() . Então, na
interseção
. Então, na
interseção ![]() devemos ter
devemos ter
![]() e
e
![]() diferenciáveis. Mas,
diferenciáveis. Mas,
![]()
![]() , a operação produto é
, a operação produto é
![]() é um grupo de Lie real de dimensão 1.
é um grupo de Lie real de dimensão 1.