


Next: Teoria de London
Up: Propriedades magnéticas reais de
Previous: Demonstração experimental do efeito
A figura acima mostra um supercondutor de superfície plana e, perto
dele, um
ímã. Vamos ver que o fato de que o campo no interior do supercondutor
tem de
ser nulo, cria uma força de repulsão entre o ímã e o
supercondutor que é
capaz de levitar o ímã. A demonstração é facil de obter usando
técnicas de
potencial.
O que acontece com um polo magnético posto diante de um plano supercondutor?
Fora do plano e do ponto onde está o polo, temos as equações
A primeira, que é válida sempre (inclusive na superfície) garante
a continuidade da componente normal de 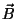 . Como
. Como 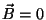 dentro
do condutor, a componente normal de
dentro
do condutor, a componente normal de  no plano é nula. Então,
resolvemos o problema assim:
no plano é nula. Então,
resolvemos o problema assim:
Isto é, trata-se de um problema de potencial. A condição de contorno
é que
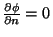 na superfície do supercondutor.
O problema está completamente determinado e a solução é única. Vamos
mostrar que ela pode ser obtida pelo método das imagens.
A superposição das duas ``cargas'' da figura satisfaz as condições do
problema.
na superfície do supercondutor.
O problema está completamente determinado e a solução é única. Vamos
mostrar que ela pode ser obtida pelo método das imagens.
A superposição das duas ``cargas'' da figura satisfaz as condições do
problema.
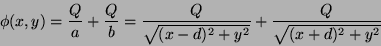 |
(26) |
É óbvio que 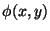 satisfaz a equação de Laplace. Sua derivada
satisfaz a equação de Laplace. Sua derivada
![\begin{displaymath}
\frac{\partial \phi}{\partial x}= -2Q\left(\frac{x-d}{[(x-d)...
...{\frac{3}{2}}}
+\frac{x+d}{[(x+d)^2+y^2]^{\frac{3}{2}}}\right)
\end{displaymath}](img77.png) |
(27) |
deve se anular em 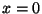 (componente normal do campo!). Logo,
(componente normal do campo!). Logo,
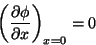 |
(28) |
É então muito fácil prever o comportamento do ímã.



Next: Teoria de London
Up: Propriedades magnéticas reais de
Previous: Demonstração experimental do efeito
Henrique Fleming
2002-04-15
(6,1)
\uput[0](1.5,0.5){{...
...5,2.5)(1.5,2.5)(1.5,2)
\uput[0](1.5,2.25){+}
\uput[0](4,2.25){-}
\end{pspicture}](img67.png)
(6,1)
\uput[0](1.5,0.5){{...
...5,2.5)(1.5,2.5)(1.5,2)
\uput[0](1.5,2.25){+}
\uput[0](4,2.25){-}
\end{pspicture}](img67.png)
(3,8)
\psline(0,4)(6,4)
\...
...(3.9,3.8){$d$}
\uput[0](1.9,3.8){$d$}
\uput[0](4.8,6.3){$(x,y)$}
\end{pspicture}](img74.png)