


Next: ``Macetes''
Up: Conceito geral de tensor
Previous: Conceito geral de tensor
Tensores de segunda ordem são, essencialmente, um certo produto de dois vetores,
como vimos no exemplo do tensor momento de inércia.
Tensores de ordem 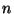 são produtos de
são produtos de 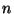 vetores. Essas quantidades aparecem
naturalmente na física. Por exemplo, a curvatura do espaço-tempo,
que, segundo Einstein, é o campo gravitacional, é um tensor de quarta
ordem. No caso geral, onde não se usam coordenadas cartesianas ortogonais,
um tensor de segunda ordem pode ser covariante, contravariante ou misto.
Chama-se tensor de segunda ordem 2 vezes contravariante ao ente
caracterizado pelas componentes
vetores. Essas quantidades aparecem
naturalmente na física. Por exemplo, a curvatura do espaço-tempo,
que, segundo Einstein, é o campo gravitacional, é um tensor de quarta
ordem. No caso geral, onde não se usam coordenadas cartesianas ortogonais,
um tensor de segunda ordem pode ser covariante, contravariante ou misto.
Chama-se tensor de segunda ordem 2 vezes contravariante ao ente
caracterizado pelas componentes 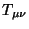 que se transformam, por
mudança de coordenadas, da forma seguinte:
que se transformam, por
mudança de coordenadas, da forma seguinte:
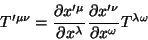 |
(71) |
isto é, como o produto de dois vetores contravariantes.
Um tensor de segunda ordem é duas vezes covariante quando suas
componentes se transformam assim:
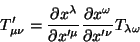 |
(72) |
ou seja, como o produto de dois vetores covariantes.
Finalmente, um tensor de segunda ordem é uma vez covariante e
uma vez contravariante quando suas componentes se transformam como
o produto de um vetor covariante por um vetor contravariante,
isto é, quando
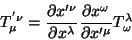 |
(73) |
Um tensor de ordem 1 é um vetor. Um tensor de ordem zero
é um escalar, ou invariante. Um exemplo d einvariante: sejam 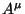 as componentes de um vetor contravariante;
as componentes de um vetor contravariante; 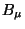 as de um vetor
covariante. Considere o produto ``contraído''
as de um vetor
covariante. Considere o produto ``contraído''
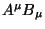 :
:
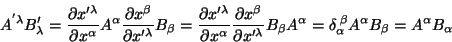 |
(74) |
O produto ``contraído''(isto é, com todos os índices repetidos)
de um vetor covariante por um contravariante é um invariante. Este é
o caso particular mais simples de uma técnica geral de construir invariantes:
contrair todos os índices de uma expressão tensorial. Veremos outros exemplos.
Subsections



Next: ``Macetes''
Up: Conceito geral de tensor
Previous: Conceito geral de tensor
Henrique Fleming
2002-04-15