


Next: About this document ...
Up: Radiação eletromagnética
Previous: Radiação eletromagnética
Os potenciais eletromagnéticos no ``calibre'' de Lorentz satisfazem
as equações
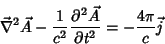 |
(43) |
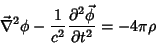 |
(44) |
Como ambas as equações têm a mesma forma, basta estudar uma
delas. Por exemplo, a Eq. 44. Note-se, primeiro, que
a equação de Poisson
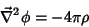 |
(45) |
é um caso particular da 44, quando o potencial
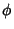 é independente do tempo. A solução da equação
de Poisson 45 é:
é independente do tempo. A solução da equação
de Poisson 45 é:
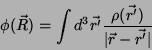 |
(46) |
e poderíamos conjecturar que a solução da 44
seria simplesmente uma modificação da 46
que consiste em introduzir a dependência temporal em 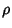 , ou
seja
, ou
seja
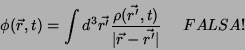 |
(47) |
No entanto, isto não é verdadeiro. A Eq. 47 está
dizendo que, mesmo que 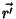 , a posição da carga, esteja
muito distante de
, a posição da carga, esteja
muito distante de 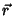 , a posição em que estamos medindo
o potencial, o valor deste no instante
, a posição em que estamos medindo
o potencial, o valor deste no instante 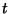 depende só do valor
da carga neste mesmo instante. Mas isto significa propagação
instantantânea! Mais razoável é supor que uma mudança na
carga em
depende só do valor
da carga neste mesmo instante. Mas isto significa propagação
instantantânea! Mais razoável é supor que uma mudança na
carga em 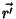 só produza efeitos em
só produza efeitos em 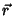 depois de um
certo intervalo de tempo, durante o qual a informação de que a
garga mudou viaja de
depois de um
certo intervalo de tempo, durante o qual a informação de que a
garga mudou viaja de 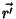 até
até 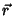 . Ora, esta viagem
dura
. Ora, esta viagem
dura
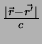 segundos, logo, seria de se
esperar que
segundos, logo, seria de se
esperar que
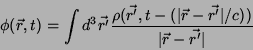 |
(48) |
e, analogamente,
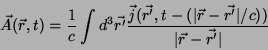 |
(49) |
Este resultado pode ser obtido resolvendo diretamente as Eqs. 43
e 44 pelo método das funções
de Green, que é apresentado no apêndice a este capítulo.
O leitor pode passar sem essa dedução, se achou razoáveis
os argumentos acima. Os potenciais dados por 48 e
49 são denominados potenciais retardados 1



Next: About this document ...
Up: Radiação eletromagnética
Previous: Radiação eletromagnética
Henrique Fleming
2001-11-29