


Next: Postulado dinâmico fundamental
Up: Dinâmica e Leis de
Previous: Dinâmica e Leis de
Apresentamos nestas notas o tratamento do princípio variacional
no estilo de Julian Schwinger. Não há nada de novo aqui: reproduzo,
essencialmente, os escritos do mestre,
comentando, quando há utilidade no comentário, alguma passagem, ou
ilustrando as idéias com algum exemplo.
Em minha opinião este
tratamento do princípio variacional é particularmente elegante
no que tange as consequências das simetrias: o teorema de Noether
é obtido de maneira muito econômica, e os geradores dos grupos
de transformações de invariância recebem o destaque devido. Isto
aproxima muito o método de Schwinger do método original de
Emmy Noether.
Isto é um trabalho em andamento. Ao poucos irei acrescentando
exemplos e generalizando as situações tratadas.
Consideraremos primeiro a mecânica quântica de um sistema com
um número finito de graus de liberdade. Sejam
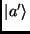 : estado do sistema na representação
: estado do sistema na representação 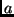 .
.
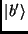 : o mesmo, na representação
: o mesmo, na representação 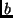 .
.
A função de transformação
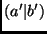 liga as
duas representações:
liga as
duas representações:
de onde segue que
e, em particular, que
Uma relação fundamental é
Se
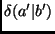 e
e
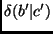 são
quaisquer variações infinitesimais, então, da relação
acima,
são
quaisquer variações infinitesimais, então, da relação
acima,
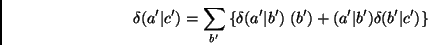 |
(1) |
e
 |
(2) |
Além disso,
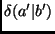 pode ser pensado como a
matriz de um operador na representação
pode ser pensado como a
matriz de um operador na representação 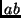 :
:
 |
(3) |
A relação acima para as variações então dá:
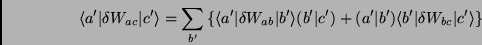 |
(4) |
o que é equivalente a
 |
(5) |
Daí segue (tomando-se 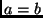 ) que
) que
 |
(6) |
e que, tomando-se 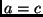 ,
,
 |
(7) |
Além disso, como
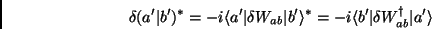 |
(8) |
e, como
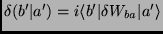 ,
temos
,
temos
 |
(9) |
ou seja, os operadores 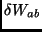 são hermiteanos.
A dinâmica, ou seja, a evolução temporal, pode ser estudada como uma seqüência
de transformações geradas pelas funções
são hermiteanos.
A dinâmica, ou seja, a evolução temporal, pode ser estudada como uma seqüência
de transformações geradas pelas funções
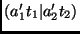 , onde as representações
se distinguem pelo tempo.
, onde as representações
se distinguem pelo tempo.
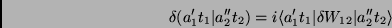 |
(10) |
e, como antes,
 |
(11) |



Next: Postulado dinâmico fundamental
Up: Dinâmica e Leis de
Previous: Dinâmica e Leis de
Henrique Fleming
2001-12-28