


Next: Campos
Up: Dinâmica e Leis de
Previous: Dinâmica
O postulado dinâmico fundamental declara que existe um operador  tal que
tal que
![\begin{displaymath}
\delta W_{12} = \delta\left[W_{12}\right]\;.
\end{displaymath}](img30.png) |
(12) |
Daí segue imediatamente que
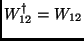 e que
e que
 |
(13) |
Se a transformação de 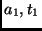 em
em 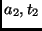 é obtida por uma sucessão de transformações
infinitesimais, temos
é obtida por uma sucessão de transformações
infinitesimais, temos
 |
(14) |
com 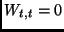 . Escrevendo
. Escrevendo
 |
(15) |
pomos
 |
(16) |
Definição: uma simetria é uma transformação que deixa inalterada
a função de transformação. Ou seja, sob uma transformação que é uma simetria,
 |
(17) |
As transformações em
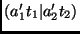 surgem de transformações
nos estados
surgem de transformações
nos estados
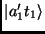 e
e
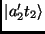 . Temos
. Temos
e, portanto,
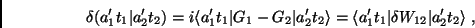 |
(20) |
o que quer dizer que
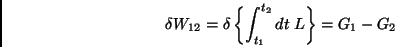 |
(21) |
ou seja, a variação da ação proveniente das transformações
depende, para a evolução física do sistema, só de quantidades nos extremos. Ora,
a variação contém ainda trmos que dependem dos instantes intermediários entre 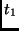 e
e 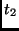 . Logo, outra maneira de formular (21) é dizer que, para variações
que se anulam nos extremos, a evolução física satisfaz a
. Logo, outra maneira de formular (21) é dizer que, para variações
que se anulam nos extremos, a evolução física satisfaz a
 |
(24) |
que é a forma usual do princípio variacional.
Suponhamos agora que as transformações geradas pelos 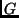 sejam simetrias. Então
sejam simetrias. Então
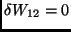 , e, em conseqüência,
, e, em conseqüência,
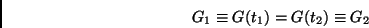 |
(25) |
ou seja, os geradores são constantes do movimento.
Quando se calcula
aparecem, além dos termos ``de superfície'', que dependem só dos instantes extremos, outros
termos, que devem, pelo prinípio dinâmico, se anular. Uma maneira de obtê-los é
restringir-se a transformações (``variações'') que se anulam nos extremos. Daí vem o usual
``prinípio de mínima ação'': a ação é estacionária para variações que se anulam nos extremos.
Subsections



Next: Campos
Up: Dinâmica e Leis de
Previous: Dinâmica
Henrique Fleming
2001-12-28
