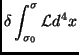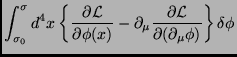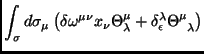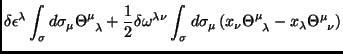Next: About this document ...
Up: Postulado dinâmico fundamental
Previous: Postulado dinâmico fundamental
Campos possuem um número infinito de graus de liberdade. Denotaremos por
os estados caracterizados por um conjunto completo de variáveis conpatíveis 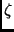 , que
são os campos, em um determinado instante, ou numa superfície de tipo espaço
, que
são os campos, em um determinado instante, ou numa superfície de tipo espaço 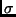 .
Como no caso anterior, temos
.
Como no caso anterior, temos
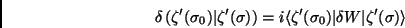 |
(26) |
Suponhamos que os observáveis sejam submetidos a uma variação
que afeta também os estados, levando-os a
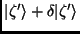 ,
com
,
com
Então,
onde 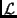 é a densidade lagrangeana.
é a densidade lagrangeana.
Exemplo: campos escalares.
Os campos são descritos por operadores 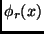 que têm propriedades de
transformação simples, sob mudanças de referencial. Seja
que têm propriedades de
transformação simples, sob mudanças de referencial. Seja 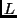 uma transformação
de Lorentz infinitesimal.
uma transformação
de Lorentz infinitesimal.
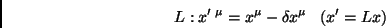 |
(30) |
 |
(31) |
 |
(32) |
A fórmula de transformação é
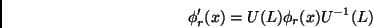 |
(33) |
 |
(34) |
Os campos mais simples são os escalares. Têm só uma componente, e
 |
(35) |
Como
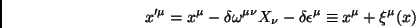 |
(36) |
e
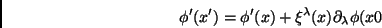 |
(37) |
temos
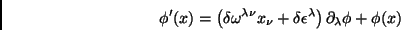 |
(38) |
logo,
![\begin{displaymath}
\phi(x)+\delta\omega^{\lambda \nu}x_\nu\partial_\lambda\phi...
...ac{1}{2}\delta\omega^{\lambda \nu}J_{\lambda \nu},\phi\right]
\end{displaymath}](img85.png) |
(39) |
o que dá,
![\begin{displaymath}
\left[P_\lambda, \phi(x)\right]=-i\partial_\lambda \phi
\end{displaymath}](img86.png) |
(40) |
e
![\begin{displaymath}
\left[J_{\lambda \nu},\phi(x)\right]=-i(x_\nu\partial_\lambda\phi-x_\lambda\partial_\nu\phi)
\end{displaymath}](img87.png) |
(41) |
Seja agora 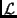 a densidade lagrangeana que é um escalar que depende de
a densidade lagrangeana que é um escalar que depende de
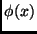 e de suas derivadas
e de suas derivadas
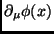 . Utilizando variações geradas por
transformações do grupo de Poincaré, a equação dinâmica básica
. Utilizando variações geradas por
transformações do grupo de Poincaré, a equação dinâmica básica
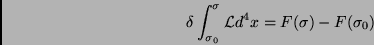 |
(42) |
vai permitir dterminar a expressão dos geradores do grupo de Poincaré
em termos dos campos 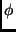 e suas derivadas.
As variações geradas por transformações de Poincaré transformam a região
e suas derivadas.
As variações geradas por transformações de Poincaré transformam a região 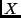 (espaço-tempo delimitado pelas superfícies de tipo espaço
(espaço-tempo delimitado pelas superfícies de tipo espaço 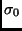 e
e 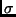 ) na
região
) na
região 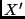 . A variação é
. A variação é
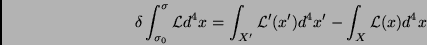 |
(43) |
Mas
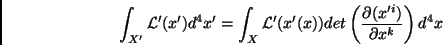 |
(44) |
Por outro lado, para a transformação
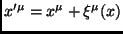 , temos
, temos
 |
(45) |
e
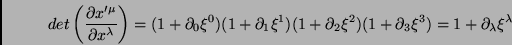 |
(46) |
o que permite escrever
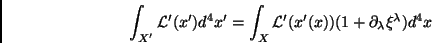 |
(47) |
e, como
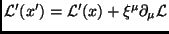 , temos
, temos
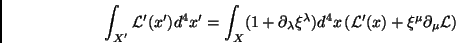 |
(48) |
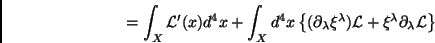 |
(49) |
Então,
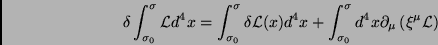 |
(50) |
Mas
o que dá
Temos ainda que
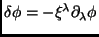 , e então
, e então
Equivalentemente,
com
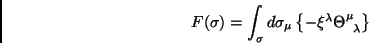 |
(56) |
Logo, o princípio dinâmico diz que
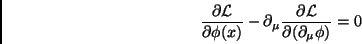 |
(57) |
Tomando os  como geradores do grupo de Poincaré, que é um grupo de simetrias
do sistema, temos
como geradores do grupo de Poincaré, que é um grupo de simetrias
do sistema, temos
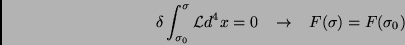 |
(58) |
e os geradores são constantes do movimento.
Como
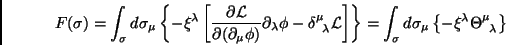 |
(59) |
temos, pondo
 |
(60) |
que
de onde se conclui que
 |
(62) |
e
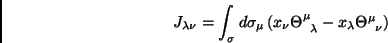 |
(63) |
sendo que
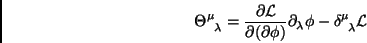 |
(64) |
é o tensor de momento-energia canônico.
As leis de conservação podem ser escritas
 |
(65) |
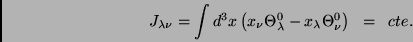 |
(66) |
O teorema de Noether é isso: dado um grupo de simetria, os geradores
desse grupo (1 para cada parâmetro) são constantes do movimento.



Next: About this document ...
Up: Postulado dinâmico fundamental
Previous: Postulado dinâmico fundamental
Henrique Fleming
2001-12-28
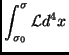
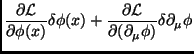
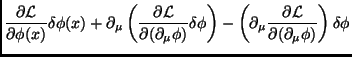
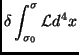
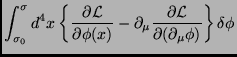
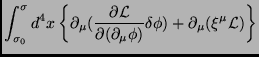
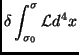
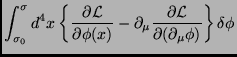
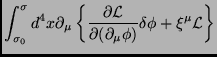
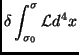
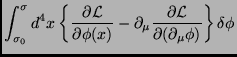
![$\displaystyle \int_{\sigma_0}^{\sigma}d^4x\partial_\mu
\left\{-\xi^\lambda\left...
...u\phi)}
\partial_\lambda\phi-\delta^\mu_{\;\;\lambda}\mathcal{L}\right]\right\}$](img114.png)