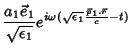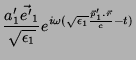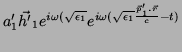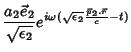Next: Refração
Up: Teoria de Maxwell
Previous: As equações
As soluções das equações para 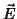 e
e 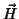 são
são
onde 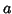 é uma constante (amplitude da onda) e os vetores
é uma constante (amplitude da onda) e os vetores 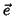 e
e
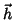 são os vetores (unitários) de polarização dos campos elétrico e
magnético, respectivamente, e estão definidos na figura. O vetor
são os vetores (unitários) de polarização dos campos elétrico e
magnético, respectivamente, e estão definidos na figura. O vetor 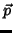 é
um vetor unitário na direção e sentido da propagação da onda.
é
um vetor unitário na direção e sentido da propagação da onda.
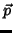 ,
, 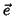 e
e 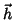 , nessa ordem, formam um triedro dextrógiro.
, nessa ordem, formam um triedro dextrógiro.
As soluções apresentadas acima são ondas planas e monocromáticas que
se propagam na matéria. Os campos incidentes são:
Os campos refletidos são
e, finalmente, os refratados são
Temos aí soluções para o meio 1 e soluções para o meio 2. A conexão
entre elas é feita através das fórmulas bem conhecidas do eletromagnetismo,
que devem ser satisfeitas nos pontos da superfície de separação
dos meios. No meios 1 e 2, os campos elétricos totais são:



Next: Refração
Up: Teoria de Maxwell
Previous: As equações
Henrique Fleming
2001-11-29
![]() e
e ![]() são
são
{$\vec{E}_i\; ,\vec{H}_i$}
\end{pspicture}](img35.png)