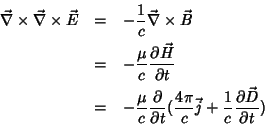Next: As soluções
Up: Teoria de Maxwell
Previous: Teoria de Maxwell
A descoberta, por Maxwell, de que a luz é uma onda
eletromagnética, foi uma das mais importantes de toda
a história da ciência. Neste capítulo veremos como,
dentro da teoria de Maxwell, se descreve a reflexão e a refração
da luz na passagem de um meio para outro, separados por um plano. Trata-se
de um problema clássico, cuja solução era conhecida séculos antes
de Maxwell. A teoria de Maxwell, ao reobter esses resultados, os
enriquecerá, fornecendo uma descrição das intensidades com que os
fenômenos em questão ocorrem, bem como importantes conseqüências,
para eles, do caráter vetorial das ondas eletromagnéticas, ou seja,
da polarização da luz. No tratamento clássico da refração, por exemplo,
determina-se a direção do raio refratado (pela lei de Snell-Descartes), mas
não se dá nenhuma informação sobre a intensidade da luz refratada
em relação à intensidade da luz incidente.
As equações de Maxwell num meio simples, cujas propriedades eletromagnéticas
podem ser sintetizadas nas constantes 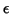 e
e 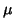 , são:
, são:
onde 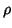 e
e 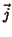 são, respectivamente, as densidades de carga ``verdadeira'',
isto é, cargas que não são de polarização, e correntes ``verdadeiras'', ou
seja, que transportam cargas macroscopicamente (excluíndo-se, portanto,
correntes eletrônicas, por exemplo).
Das equações de Maxwell se obtêm equações de onda. Tomando o
são, respectivamente, as densidades de carga ``verdadeira'',
isto é, cargas que não são de polarização, e correntes ``verdadeiras'', ou
seja, que transportam cargas macroscopicamente (excluíndo-se, portanto,
correntes eletrônicas, por exemplo).
Das equações de Maxwell se obtêm equações de onda. Tomando o 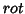 da
Eq.(3), tem-se:
da
Eq.(3), tem-se:
Suponhamos que 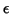 e
e 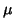 sejam constantes, e que
sejam constantes, e que 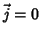 . Temos
então, como
. Temos
então, como
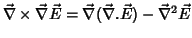 e
e
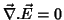 ,
,
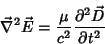 |
(5) |
ou, usando
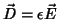 ,
,
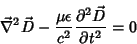 |
(6) |
que mostra que se tem uma onda com velocidade de propagação dada por
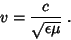 |
(7) |
Um cálculo análogo para o campo magnético leva a
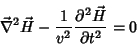 |
(8) |
Nos meios transparentes, que são os que nos interessam neste capítulo,
tem-se, em geral, 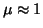 . Por causa disso omitiremos
. Por causa disso omitiremos 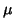 das
nossas fórmulas, a seguir.
das
nossas fórmulas, a seguir.



Next: As soluções
Up: Teoria de Maxwell
Previous: Teoria de Maxwell
Henrique Fleming
2001-11-29
![]() e
e ![]() , são:
, são: