


Next: Grupo de Lie
Up: Recordação de material básico
Previous: Produto de topologias
O conceito de variedade produto será essencial no estudo dos
grupos de Lie. Uma variedade diferenciável é denotada por
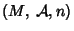 , onde
, onde 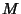 é um espaço topológico,
é um espaço topológico,
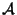 é um atlas e
é um atlas e 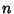 é a dimensão da variedade.
Sejam
é a dimensão da variedade.
Sejam
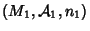 e
e
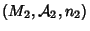 duas
variedades. A variedade produto é definida assim:
é a variedade diferenciável
duas
variedades. A variedade produto é definida assim:
é a variedade diferenciável
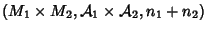 onde os símbolos significam:
onde os símbolos significam:
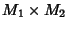 : é o espaço topológico dos pares
: é o espaço topológico dos pares
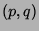 , com
, com 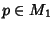 e
e 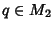 , dotado da topologia produto.
, dotado da topologia produto.
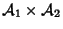 :é o ``produto de atlas'',
definido assim: seja
:é o ``produto de atlas'',
definido assim: seja 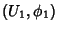 uma carta de
uma carta de 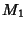 , e
, e 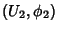 uma carta de
uma carta de 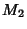 .
.
Então
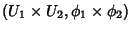 será uma carta
de
será uma carta
de
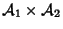 , onde
, onde
é definido como
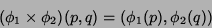 |
(3) |
Henrique Fleming
2001-12-26