Next: O teorema de Noether
Up: Simetrias na Física Clássica
Previous: Simetrias na Física Clássica
O sistema que vamos estudar é caracterizado por uma densidade
lagrangeana 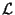 . Por enquanto estaremos restritos ao
espaço-tempo de Minkowski. A ação clássica, então, é:
. Por enquanto estaremos restritos ao
espaço-tempo de Minkowski. A ação clássica, então, é:
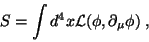 |
(1) |
onde tomamos 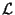 como função de alguns campos
como função de alguns campos
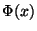 e de suas primeiras derivadas
e de suas primeiras derivadas
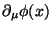 .
Começaremos supondo que os campos
.
Começaremos supondo que os campos 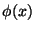 sejam escalares, para
revelar mais claramente a estrutura do método.
sejam escalares, para
revelar mais claramente a estrutura do método.
Uma transformação infinitesimal dos campos
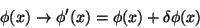 |
(2) |
induz uma variação infinitesimal
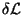 na
densidade lagrangeana. Diz-se que a transformação é uma
simetria quando é possível mostrar, sem
o uso das equações do movimento, que
na
densidade lagrangeana. Diz-se que a transformação é uma
simetria quando é possível mostrar, sem
o uso das equações do movimento, que
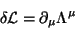 |
(3) |
onde 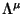 é um quadrivetor.
é um quadrivetor.
Comentários:
(i)``Sem o uso das equções de movimento'', ou seja, para todas
as configurações, e não somente a configuração que a
natureza escolhe.
(ii)É isto que per,ite que o conceito (de simetria) tenha valor na
mecânica quântica, pois ali não há a ``configuração que
a natureza escolhe''. No formalismo de Feynman o propagador é uma
soma sobre todas as configurações concebíveis. Logo, a
simetria, como definida no texto, é uma simetria do propagador.
Exemplo 1:
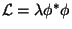 (O asterisco
(O asterisco 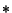 representa o
complexo conjugado).
representa o
complexo conjugado).
A transformação infinitesimal
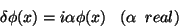 |
(4) |
é uma simetria. de fato,
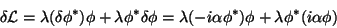 |
(5) |
ou
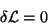 |
(6) |
significando que 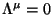 . Simetrias desse tipo
(
. Simetrias desse tipo
(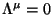 ) são ditas simetrias internas.
) são ditas simetrias internas.
Exemplo 2: translações.
Uma translação das coordenadas
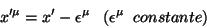 |
(7) |
induz nos campos 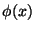 uma transformação
uma transformação 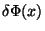 que
calcularemos agora. Como
que
calcularemos agora. Como 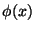 é escalar,
é escalar,
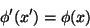 |
(8) |
Por outro lado, expansão em potências de 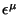 dá
dá
de maneira que
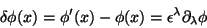 |
(10) |
Suponha que
o que mostra que translações são simetrias do sistema descrito
pela lagrangeana exibida.



Next: O teorema de Noether
Up: Simetrias na Física Clássica
Previous: Simetrias na Física Clássica
Henrique Fleming
2002-09-06
![]() (O asterisco
(O asterisco ![]() representa o
complexo conjugado).
representa o
complexo conjugado).