


Next: Exemplo 1: translações
Up: Simetrias na Física Clássica
Previous: Introdução
O teorema de Noether afirma que a cada simetria contínua
corresponde uma corrente que satisfaz uma equação de
continuidade, ou, equivalentemente, uma quantidade que é conservada.
Além disso, o teorema fornece uma expressão explícita para a
corrente.
Seja 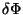 uma transformação de simetria. Então existe
uma transformação de simetria. Então existe
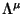 tal que
tal que
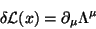 |
(14) |
Um cálculo independente de
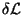 , desta vez usando as
equações de movimento, será realizado agora.
, desta vez usando as
equações de movimento, será realizado agora.
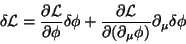 |
(15) |
As equações de movimento são
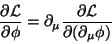 |
(16) |
que, usadas em (15), dão
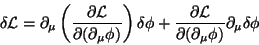 |
(17) |
ou seja,
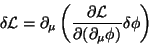 |
(18) |
Subtraíndo (18) de (14), tem-se
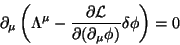 |
(19) |
que é o teorema de Noether. A quantidade
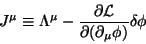 |
(20) |
é a corrente de Noether associada à simetria 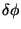 .
.
Subsections



Next: Exemplo 1: translações
Up: Simetrias na Física Clássica
Previous: Introdução
Henrique Fleming
2002-09-06
![]() uma transformação de simetria. Então existe
uma transformação de simetria. Então existe
![]() tal que
tal que