


Next: Bibliography
Up: Apêndice:O Método do Ponto
Previous: Apêndice:O Método do Ponto
Considere a função
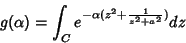 |
(70) |
onde o contorno 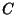 , ilustrado na figura, começa e termina no eixo
real, em
, ilustrado na figura, começa e termina no eixo
real, em 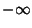 e
e 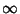 , respectivamente.
A função é da forma
, respectivamente.
A função é da forma
com 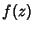 dada por
dada por
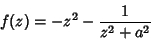 |
(71) |
Um cálculo simples mostra que
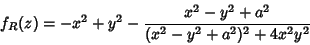 |
(72) |
enquanto que
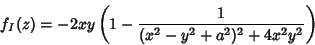 |
(73) |
Como a integral converge, já que 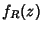 tende a zero para
tende a zero para
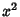 tendendo a infinito com
tendendo a infinito com 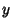 limitado, as singularidades de
limitado, as singularidades de
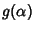 são as singularidades do integrando. A função
são as singularidades do integrando. A função 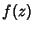 tem polos em
tem polos em 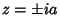 . O contorno
. O contorno 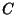 está entre
está entre 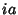 e o eixo
real. Logo, podemos deformá-lo a vontade nessa região.
O ponto sela é determinado pela equação
e o eixo
real. Logo, podemos deformá-lo a vontade nessa região.
O ponto sela é determinado pela equação
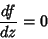 |
(74) |
ou seja,
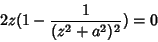 |
(75) |
que tem a solução
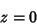 |
(76) |
A derivada segunda de 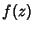 é
é
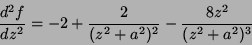 |
(77) |
e, no ponto sela, tem o valor
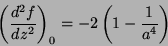 |
(78) |
A família de curvas 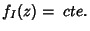 é muito complicada. No entanto,
para a curva
é muito complicada. No entanto,
para a curva  com
com 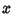 qualquer, temos
qualquer, temos 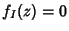 , e, portanto,
constante. Como esta curva passa por
, e, portanto,
constante. Como esta curva passa por 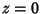 , ela é a curva de máximo
aclive procurada. Ou seja, para o cálculo do valor assintótico
de
, ela é a curva de máximo
aclive procurada. Ou seja, para o cálculo do valor assintótico
de 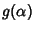 é conveniente deformar o contorno de maneira a fazê-lo
coincidir com o eixo real. Portanto, temos
é conveniente deformar o contorno de maneira a fazê-lo
coincidir com o eixo real. Portanto, temos
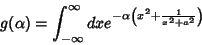 |
(79) |
Podemos agora expandir 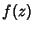 em torno do ponto sela. Como
a derivada primeira é nula no ponto sela, resulta que
em torno do ponto sela. Como
a derivada primeira é nula no ponto sela, resulta que
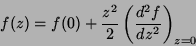 |
(80) |
o que dá
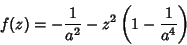 |
(81) |
Temos então para 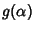 :
:
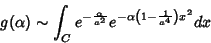 |
(82) |
e agora a integral pode ser calculada facilmente. De fato,
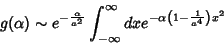 |
(83) |
Usando o resultado conhecido ( integral de Gauss)
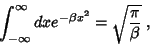 |
(84) |
obtemos
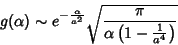 |
(85) |
que é o resultado procurado, válido para grandes valores de
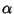 .
.



Next: Bibliography
Up: Apêndice:O Método do Ponto
Previous: Apêndice:O Método do Ponto
Henrique Fleming
2001-11-22
{$ia$}
\psdots[dotstyle=*](5,5.5)
\end{pspicture}](img209.png)