


Next: Exemplo simples
Up: O Famoso Apêndice de
Previous: Comportamento Assintótico
Seja
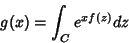 |
(64) |
onde 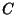 é um contorno aberto com a propriedade de que
é um contorno aberto com a propriedade de que
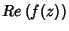 tenda a
tenda a 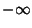 em ambas as suas extremidades. A partir de agora
escreveremos o número complexo
em ambas as suas extremidades. A partir de agora
escreveremos o número complexo 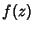 assim, decomposto em sua parte
real e imaginária:
assim, decomposto em sua parte
real e imaginária:
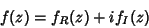 |
(65) |
Consideremos valores positivos e grandes de 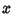 . Como
. Como
e
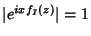 , o módulo do integrando na Eq.(64)
é dado por
, o módulo do integrando na Eq.(64)
é dado por 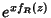 . Esta função, para um dado
. Esta função, para um dado 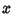 , varia de um valor
máximo, atingido quando
, varia de um valor
máximo, atingido quando 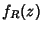 é máximo, até zero, pelo menos nos
extremos. Para
é máximo, até zero, pelo menos nos
extremos. Para 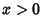 e muito grande, temos um ``pico'' muito elevado, de
onde o valor da integral cai rapidamente para o ``vale'' (região de baixos
valores). Além disso, podemos utilizar a possibilidade de deformar o
contorno, para fazer com que ele fique ``a maior parte do tempo'' nos vales,
subindo ao pico pelo caminho mais íngreme. Desta maneira, apenas uma pequena
parte do contorno contribuirá efetivamente para a integral. O método do
ponto sela é isto: achar o contorno mais íngreme, passando pelo pico. Note
que são os valores muito grandes de
e muito grande, temos um ``pico'' muito elevado, de
onde o valor da integral cai rapidamente para o ``vale'' (região de baixos
valores). Além disso, podemos utilizar a possibilidade de deformar o
contorno, para fazer com que ele fique ``a maior parte do tempo'' nos vales,
subindo ao pico pelo caminho mais íngreme. Desta maneira, apenas uma pequena
parte do contorno contribuirá efetivamente para a integral. O método do
ponto sela é isto: achar o contorno mais íngreme, passando pelo pico. Note
que são os valores muito grandes de 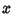 que acentuam essas propriedades
extremas. Logo, o método se presta para calcular valores assintóticos.
A determinação do caminho mais íngreme passando pelo pico pode ser feita
assim: considere as curvas de nível de
que acentuam essas propriedades
extremas. Logo, o método se presta para calcular valores assintóticos.
A determinação do caminho mais íngreme passando pelo pico pode ser feita
assim: considere as curvas de nível de 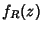 , ou seja, as curvas
ao longo das quais
, ou seja, as curvas
ao longo das quais 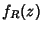 é constante. O que procuramos são as curvas
que cortem essas curvas de nível ortogonalmente: são estas as que
``sobem mais rapidamente''. Ora, essas curvas são, como se sabe da
teoria de funções analíticas de uma variável complexa, as curvas ao
longo das quais
é constante. O que procuramos são as curvas
que cortem essas curvas de nível ortogonalmente: são estas as que
``sobem mais rapidamente''. Ora, essas curvas são, como se sabe da
teoria de funções analíticas de uma variável complexa, as curvas ao
longo das quais 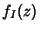 é constante. Logo, temos de achar a curva
dessa família que passa pelo ``pico''. No ``pico'' (que é o ponto
sela) temos
é constante. Logo, temos de achar a curva
dessa família que passa pelo ``pico''. No ``pico'' (que é o ponto
sela) temos
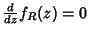 . Vimos agora que, pelo caminho escolhido,
. Vimos agora que, pelo caminho escolhido,
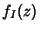 é constante, e, portanto,
é constante, e, portanto,
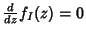 . Logo, o
ponto sela satisfaz a equação complexa
. Logo, o
ponto sela satisfaz a equação complexa
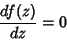 |
(66) |
Seja 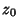 o ponto em que essa equação é satisfeita (pode haver vários).
Expandindo a função em torno desse ponto, temos
o ponto em que essa equação é satisfeita (pode haver vários).
Expandindo a função em torno desse ponto, temos
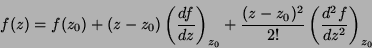 |
(67) |
mais termos de ordem superior. A derivada primeira é nula, por definição
de ponto sela. Logo, temos, para a parte real do integrando,
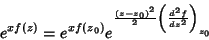 |
(68) |
com
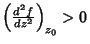 , ao longo do
contorno, por ser um máximo de
, ao longo do
contorno, por ser um máximo de 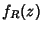 . Logo,
. Logo,
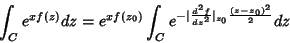 |
(69) |
que, em geral, por ser a integral de uma gaussiana, pode ser calculada
facilmente.
Subsections



Next: Exemplo simples
Up: O Famoso Apêndice de
Previous: Comportamento Assintótico
Henrique Fleming
2001-11-22