


Next: A Lei de Wien
Up: Max Planck
Previous: Max Planck
Desde a descoberta de Kirchhoff vários resultados parciais importantes
tinham sido obtidos, por alguns dos melhores físicos de então5. Primeiro, Boltzmann obteve
o resultado empírico de Stefan, de que a densidade de energia
da radiação no equilíbrio dependia da temperatura na forma
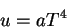 |
(3) |
onde 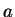 é uma constante. Para obter este resultado, Boltzmann usou
a relação de Maxwell
é uma constante. Para obter este resultado, Boltzmann usou
a relação de Maxwell
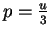 , que dá a pressão da
radiação em termos da densidade de energia. Em um cilindro provido
de um êmbolo existe radiação em equilíbrio à temperatura
T. O volume do cilindro é
, que dá a pressão da
radiação em termos da densidade de energia. Em um cilindro provido
de um êmbolo existe radiação em equilíbrio à temperatura
T. O volume do cilindro é 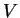 . A pressão da radiação faz com que
o êmbolo se mova lentamente, realizando o trabalho
. A pressão da radiação faz com que
o êmbolo se mova lentamente, realizando o trabalho 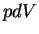 . A energia
total da radiação sendo
. A energia
total da radiação sendo 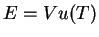 , temos
, temos
e a entropia da radiação variará de
Por consistência, devemos ter
de onde segue que
ou ainda
e, finalmente,
Êste trabalho foi considerado uma ``pérola''da termodinâmica,
por sua simplicidade e audácia. De fato, a radiação é tratada como um
gás, e uma entropia é associada a ela. Note-se ainda que a existência da
pressão da radiação, e a veracidade da fórmula de Maxwell, só
viriam a ser comprovadas experimentalmente em 1905, por Lebedev.



Next: A Lei de Wien
Up: Max Planck
Previous: Max Planck
Henrique Fleming
2002-04-13