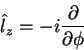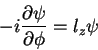Next: Autofunções simultâneas do momento
Up: Autofunções do momento angular
Previous: Autofunções do momento angular
As autofunções de 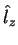 são funções
são funções 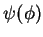 tais que
tais que
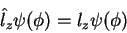 |
(89) |
onde 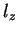 é um número. Omitimos aqui, por simplicidade, as outras
variáveis,
é um número. Omitimos aqui, por simplicidade, as outras
variáveis, 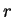 e
e 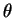 , de que a função
, de que a função 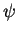 em geral depende
porque são irrelevantes para este problema. Como
em geral depende
porque são irrelevantes para este problema. Como
temos, para a Eq.(89),
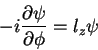 |
(90) |
cuja solução é
Devemos ainda ter
o que exige que
ou seja, que 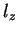 seja um número inteiro. Vamos denotá-lo por
seja um número inteiro. Vamos denotá-lo por
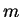 . Então,
. Então,
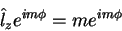 |
(91) |
que é satisfeita para qualquer 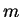 inteiro,
inteiro,
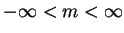 . Normalizando, temos
. Normalizando, temos
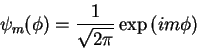 |
(92) |



Next: Autofunções simultâneas do momento
Up: Autofunções do momento angular
Previous: Autofunções do momento angular
Henrique Fleming
2003-03-30