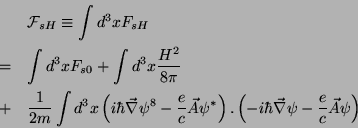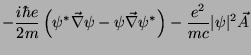Equação para $\vec{A}$

Variando-se a expressão para a energia livre do condutor em relação a 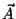$\vec{A}$, obtém-se a equação de movimento para o potencial vetor. A expressão é:

$$\begin{eqnarray*} & & \mathcal{F}_{sH} \equiv \int d^3x F_{sH}\\ & = & \int d^3... ...ht).\left( -i\hbar\vec{\nabla}\psi-\frac{e}{c}\vec{A}\psi\right) \end{eqnarray*}$$

que abreviaremos assim:

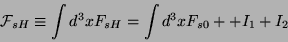$$\mathcal{F}_{sH} \equiv \int d^3x F_{sH}= \int d^3x F_{s0} + + I_1 + I_2$$ (182)

Um cálculo simples leva a

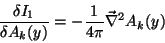$$\frac{\delta I_1}{\delta A_{k}(y)}=-\frac{1}{4\pi}\vec{\nabla}^2A_{k}(y)$$ (183)

enquanto que

$$\frac{\delta I_{2}}{\delta \vec{A}}=\frac{1}{2m} \left[-\fra... ...c{\nabla}\psi)+ \frac{2e^2}{c^2}\vert\psi\vert^2\vec{A}\right]$$ (184)

logo, a variação total igualada a zero é

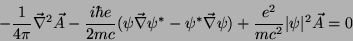$$-\frac{1}{4\pi}\vec{\nabla}^2\vec{A}-\frac{i\hbar e}{2mc}(\p... ...^*\vec{\nabla}\psi)+ \frac{e^2}{mc^2}\vert\psi\vert^2\vec{A}=0$$ (185)

ou

$$\vec{\nabla}^2\vec{A} = -\frac{4\pi}{c}\vec{j}$$ (186)

$$\vec{j} = -\frac{i\hbar e}{2m}\left(\psi^*\vec{\nabla}\psi-\psi\vec{\nabla}\psi^*\right)- \frac{e^2}{mc}\vert\psi\vert^2\vec{A}$$ (187)

A solução do problema de determinar a distribuição do campo e da corrente em um supercondutor é então reduzido à integração das equações

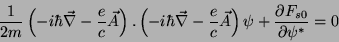$$\frac{1}{2m}\left(-i\hbar \vec{\nabla}-\frac{e}{c}\vec{A}\ri... ...c}\vec{A}\right)\psi+\frac{\partial F_{s0}}{\partial \psi^*}=0$$ (188)

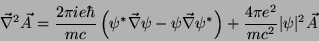$$\vec{\nabla}^2\vec{A}=\frac{2\pi i e \hbar}{mc}\left(\psi^*\... ...la}\psi^*\right)+ \frac{4\pi e^2}{mc^2}\vert\psi\vert^2\vec{A}$$ (189)

com a condição de contorno

$$\vec{n}.\left[-i\hbar \vec{\nabla}\psi -\frac{e}{c}\vec{A}\psi\right]=0$$ (190)

na superfície do condutor.