


Next: Equação para
Up: Teoria da supercondutividade de
Previous: Argumento de Rose-Innes, Rhoderic
Na ausência de campo magnético a transição para o estado supercondutor é de segunda ordem.
O parâmetro de ordem, denotado por 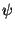 , será tal que
, será tal que
A idéia de partida é que 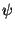 representa uma função de onda efetiva
dos elétrons supercondutores. Logo, a fase de
representa uma função de onda efetiva
dos elétrons supercondutores. Logo, a fase de 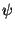 não deve ser determinável,
isto é, nas quantidades observáveis devem ocorrer apenas combinações de
não deve ser determinável,
isto é, nas quantidades observáveis devem ocorrer apenas combinações de
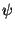 e
e 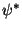 invariantes pela transformação
invariantes pela transformação
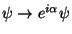 ,
sendo
,
sendo 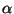 um número real. A normalização é, por enquanto, arbitrária.
um número real. A normalização é, por enquanto, arbitrária.
Considere um supercondutor uniforme na ausência de um campo magnético, e suponha que que 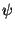 seja independente da posição . De acordo com a teoria das transições de fase de segunda
ordem, temos, para
seja independente da posição . De acordo com a teoria das transições de fase de segunda
ordem, temos, para 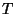 suficientemente próximo de
suficientemente próximo de 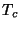 ,
,
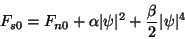 |
(159) |
onde 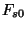 e
e 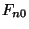 são as energias livres (a campo externo zero) da fase supercondutora
e normal, respectivamente, e
são as energias livres (a campo externo zero) da fase supercondutora
e normal, respectivamente, e 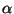 e
e 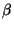 são funções da temperatura que têm
as propriedades gerais:
são funções da temperatura que têm
as propriedades gerais:
No equilíbrio, naturalmente,
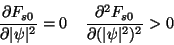 |
(164) |
sto é
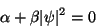 |
(165) |
dando
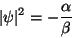 |
(166) |
Usando
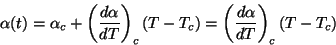 |
(167) |
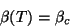 |
(168) |
temos
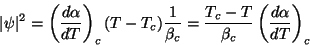 |
(169) |
e
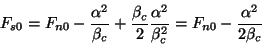 |
(170) |
Como vimos anteriormente,
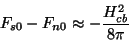 |
(171) |
logo,
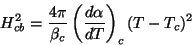 |
(172) |
que é uma relação muito bem verificada experimentalmente.
Examinemos agora o efeito, sobre o condutor, de um campo magnético independente do tempo.
Para se obter 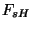 é preciso somar a
é preciso somar a 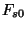 duas contribuições :
duas contribuições :
(1) A energia do campo:
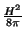
(2) A energia proveniente do aparecimento possível de um gradiente de 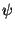 , por influência
do campo externo.
, por influência
do campo externo.
Vamos estimar esta segunda energia. Ela é função do gradiente de 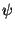 , e deve ter a
estrutura
, e deve ter a
estrutura
![\begin{displaymath}
f\left[\vec{\nabla}\psi^*.\vec{\nabla}\psi\right] \; .
\end{displaymath}](img370.png) |
(173) |
Para pequenos valores de
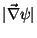 , podemos escrever
, podemos escrever
![\begin{displaymath}
f\left[\vec{\nabla}\psi^*.\vec{\nabla}\psi\right]=\frac{\hbar^2}{2m}\vert\vec{\nabla}\psi\vert^2
+\ldots
\end{displaymath}](img372.png) |
(174) |
onde 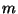 é um parâmetro. O sistema deve, contudo, ser gauge-invariante, e isto implica
em que a dependência seja em
é um parâmetro. O sistema deve, contudo, ser gauge-invariante, e isto implica
em que a dependência seja em
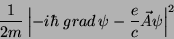 |
(175) |
Logo, em primeira aproximação ,
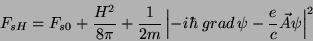 |
(176) |
A equação para 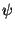 pode agora ser obtida impondo-se que
pode agora ser obtida impondo-se que
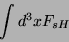 |
(177) |
seja estacionário por variações de 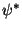 .
A energia livre total é
.
A energia livre total é
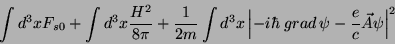 |
(178) |
Desses termos, só o último depende de 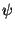 . Escrito em detalhe, ele é:
. Escrito em detalhe, ele é:
Isto é, a parte da energia dependente de 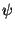 é:
é:
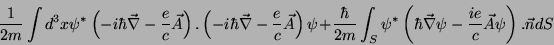 |
(179) |
Derivando em relação a 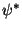 e igualando a zero, temos
e igualando a zero, temos
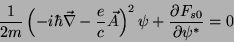 |
(180) |
e
![\begin{displaymath}
\vec{n}.\left[-i\hbar\vec{\nabla}-\frac{e}{c}\vec{A}\psi \right]=0 \;
,
\end{displaymath}](img380.png) |
(181) |
sendo a primeira interpretada como a equação de movimento, e a
segunda como uma condição de contorno.
Subsections



Next: Equação para
Up: Teoria da supercondutividade de
Previous: Argumento de Rose-Innes, Rhoderic
Henrique Fleming
2002-04-15
![]() seja independente da posição . De acordo com a teoria das transições de fase de segunda
ordem, temos, para
seja independente da posição . De acordo com a teoria das transições de fase de segunda
ordem, temos, para ![]() suficientemente próximo de
suficientemente próximo de ![]() ,
,
![]() é preciso somar a
é preciso somar a ![]() duas contribuições :
duas contribuições :
![]()
![]() , por influência
do campo externo.
, por influência
do campo externo.
![]() , e deve ter a
estrutura
, e deve ter a
estrutura
![\begin{eqnarray*}
& &\frac{1}{2m}\int d^3x\left(i\hbar
\vec{\nabla}\psi^*-\frac{...
...ec{\nabla}\psi)+
\frac{e^2}{c^2}\vec{A}\psi^*.\vec{A}\psi\right]
\end{eqnarray*}](img377.png)