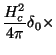Next: Apêndice
Up: Problema unidimensional
Previous: Comparação com as equações
Em um material homogêneo sob a ação de um campo magnético
com uma direção fixa, supomos a existência de uma fase normal
e uma supercondutora. A passagem de uma a outra se dá numa camada
pouco espessa que será tratada como uma superfície. Seja 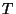 a
temperatura. Vamos calcular a energia livre por unidade de volume na
região de transição. Partindo da fase supercondutora
(
a
temperatura. Vamos calcular a energia livre por unidade de volume na
região de transição. Partindo da fase supercondutora
(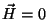 ) em direção à fase normal, iremos encontrando
campos cada vez maiores. A fase normal será encontrada quando
) em direção à fase normal, iremos encontrando
campos cada vez maiores. A fase normal será encontrada quando
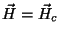 . Na reião próxima e anterior a esta, qual
é a energia livre por unidade de volume? Numa região propriamente
swpercondutora na presença de uma campo magnético externo
. Na reião próxima e anterior a esta, qual
é a energia livre por unidade de volume? Numa região propriamente
swpercondutora na presença de uma campo magnético externo
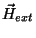 , tem-se
, tem-se
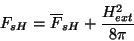 |
(221) |
o que quer dizer que a energia interna do supercondutor contém um
termo que é a energia necessária para manter o campo fora dele. Na
região de transição, o campo externo é 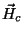 , e o
campo interno não é nulo, e sim
, e o
campo interno não é nulo, e sim 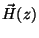 .
Logo, a energia por unidade de volume é
.
Logo, a energia por unidade de volume é
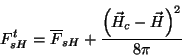 |
(222) |
exibindo-se o termo necessário para cancelar o campo
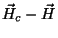 . Então,
. Então,
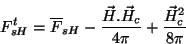 |
(223) |
Considere a quantidade
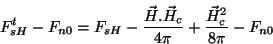 |
(224) |
que tem as propriedades:
(1)Na fase supercondutora,
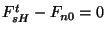 . De fato, ali,
. De fato, ali,
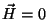 , logo,
, logo,
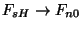 , e
, e
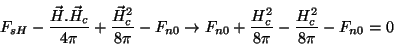 |
(225) |
Logo, a quantidade
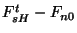 só é diferente de zero na
região de transição entre as fases. Definimos
só é diferente de zero na
região de transição entre as fases. Definimos
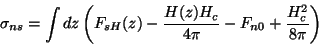 |
(226) |
senda a integração estendida à região de transição,
como a densidade de energia de superfície. Usando as
equações
temos
![\begin{displaymath}
\sigma_{ns}=\int
dz\left[\alpha\psi^2+\frac{\beta}{2}\psi^4+...
...{2m
c^2}A^2\psi^2 +\frac{H^2}{8\pi}-\frac{H_{c}H}{4\pi}\right]
\end{displaymath}](img456.png) |
(229) |
onde se usou
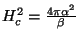 .
.
Vamos introduzir uma nova notação, em termos dos parâmetros
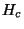 ,
, 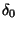 ,
, 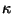 , definidos assim:
, definidos assim:
Introduzindo novas variáveis
as equações são escritas
Se 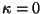 , temos
, temos
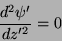 |
(241) |
que, com a condição de contorno (neste caso,
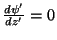 na superfície), dá
na superfície), dá
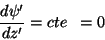 |
(242) |
Logo,
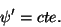 |
(243) |
e, em particular,
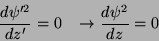 |
(244) |
Isto dá o significado do parâmetro 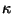 . O inverso dele mede
essencialmente a distância típica em que a variação de
. O inverso dele mede
essencialmente a distância típica em que a variação de
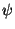 é grande.
é grande.
Vamos agora examinar a densidade superficial de energia em dois casos
extremos:
(1)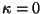 - densidade de energia positiva-
- densidade de energia positiva- 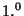 tipo.
tipo.
(2)
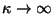 - a equação
- a equação
![\begin{displaymath}
\frac{d^2\psi'}{dz'^2}=\kappa^2\left[-(1-A'^2)\psi'+ \psi'^3\right]
\end{displaymath}](img491.png) |
(245) |
dá
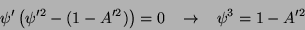 |
(246) |
Levando isto à expressão para a energia superficial, tem-se
isto é, a energia de superfície é negativa. Logo, há uma
tendência para o aumento da superfície, o que acarreta uma
penetração do campo magnético no material. Condutores deste
tipo são chamados supercondutores do 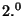 tipo(Abrikozov, 1957).
tipo(Abrikozov, 1957).



Next: Apêndice
Up: Problema unidimensional
Previous: Comparação com as equações
Henrique Fleming
2002-04-15
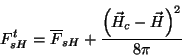
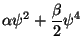
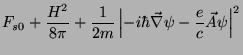
![\begin{displaymath}
\sigma_{ns}=\int
dz\left[\alpha\psi^2+\frac{\beta}{2}\psi^4+...
...{2m
c^2}A^2\psi^2 +\frac{H^2}{8\pi}-\frac{H_{c}H}{4\pi}\right]
\end{displaymath}](img456.png)
![]() ,
, ![]() ,
, ![]() , definidos assim:
, definidos assim:
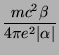
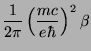
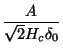
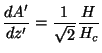
![$\displaystyle \frac{H_{c}^2}{4\pi}\delta_{0}\int\left[
\frac{1}{2}-(1-A'^2)\psi...
...rac{1}{2}\psi'^4+\frac{1}{\kappa^2}
\left(\frac{d\psi'}{dz'}\right)^2\right]dz'$](img481.png)
![$\displaystyle + \frac{H_{c}^2}{4\pi}\delta_{0}\int\left[\left(\frac{dA'}{dz'}\right)^2
-2\left(\frac{dA'}{dz'}\right)_{c}\left(\frac{dA'}{dz'}\right)\right]dz'$](img482.png)
![]() . O inverso dele mede
essencialmente a distância típica em que a variação de
. O inverso dele mede
essencialmente a distância típica em que a variação de
![]() é grande.
é grande.
![]() - densidade de energia positiva-
- densidade de energia positiva- ![]() tipo.
tipo.
![]() - a equação
- a equação