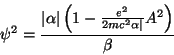Next: Energia de superfície em
Up: Problema unidimensional
Previous: A corrente
À equação (212) corresponde, na teoria de London, a
equação
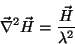 |
(213) |
que, no nosso caso, é:
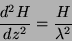 |
(214) |
Derivando a eq.(212), temos
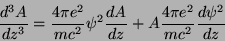 |
(215) |
Se 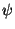 é aproximadamente constante, temos
é aproximadamente constante, temos
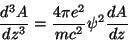 |
(216) |
e, pondo
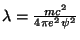 e levando em conta
que
e levando em conta
que
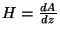 ,
,
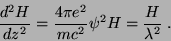 |
(217) |
Segundo London,
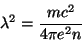 |
(218) |
onde 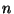 é o número de elétrons por unidade de volume, em
perfeita analogia com a teoria de Ginzburg-Landau. Note-se ainda que,
pondo-se
é o número de elétrons por unidade de volume, em
perfeita analogia com a teoria de Ginzburg-Landau. Note-se ainda que,
pondo-se
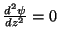 na equação para
na equação para 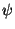 ,
tem-se
,
tem-se
![\begin{displaymath}
\psi\left[\frac{2m}{\hbar^2}\vert\alpha\vert\left(1-\frac{e^...
...\alpha\vert}A^2\right)-\frac{2m}{\hbar^2}\beta \psi^2\right]=0
\end{displaymath}](img435.png) |
(219) |
de onde sai que
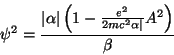 |
(220) |
isto é, o comprimento de penetração 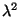 na teoria de
Ginzburg-Landau é uma função do campo, como previsto pela
experiência.
na teoria de
Ginzburg-Landau é uma função do campo, como previsto pela
experiência.



Next: Energia de superfície em
Up: Problema unidimensional
Previous: A corrente
Henrique Fleming
2002-04-15