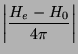Next: Histerese no modelo de
Up: Primeiras teorias
Previous: Primeiras teorias
Segundo esta teoria, um supercondutor é um condutor ôhmico de resistividade
nula, ou, de condutividade infinita. Condutores ôhmicos satisfazem a equação
constitutiva
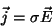 |
(1) |
o que implica numa potência dissipativa
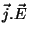 . Os supercondutores
não apresentam dissipação , logo, dentro deles, segundo esta teoria,
. Os supercondutores
não apresentam dissipação , logo, dentro deles, segundo esta teoria,
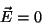 |
(2) |
o que é também consistente com a condutividade infinita e corrente finita
na equação (1).
Pela equação de Maxwell
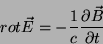 |
(3) |
temos, então, que, dentro do condutor,
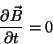 |
(4) |
Seja 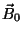 o valor do campo magnético dentro do condutor no instante
em que este perdeu a resistência. Então,
o valor do campo magnético dentro do condutor no instante
em que este perdeu a resistência. Então,
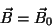 |
(5) |
enquanto o material for supercondutor.
Vamos supor sempre que o supercondutor tenha 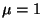 , o que é bem verificado
experimentalmente.
, o que é bem verificado
experimentalmente.
Então
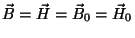 Este resultado mostra que, quando
o material se torna supercondutor, o campo magnético em seu interior é
``congelado'' no valor
Este resultado mostra que, quando
o material se torna supercondutor, o campo magnético em seu interior é
``congelado'' no valor 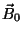 . Alterando-se o campo magnético
externo (sem atingir o campo crítico), aparecerão então
correntes superficiais que impedirão que o campo no interior se altere.
Note-se que, como
. Alterando-se o campo magnético
externo (sem atingir o campo crítico), aparecerão então
correntes superficiais que impedirão que o campo no interior se altere.
Note-se que, como
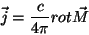 |
(6) |
temos também que, em qualquer instante,
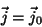 |
(7) |
com
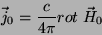 |
(8) |
Se correntes externas forem introduzidas no condutor perfeito, elas
fluirão como correntes superficiais, deixando a distribuição
volumétrica inalterada.
O cálculo das correntes superficiais é bastante simples. A equação
de Maxwell relevante é
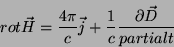 |
(9) |
No caso estático temos
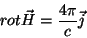 |
(10) |
A versão integral dessa equação é
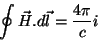 |
(11) |
onde 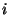 é a corrente que atravessa o contorno orientado como na
figura.
é a corrente que atravessa o contorno orientado como na
figura.
(6,0)(6,2)(0,2)(0,0)
\psl...
...}
\uput[0](4.2,0.7){$\vec{H}_{0}$}
\uput[0](2.7,1.3){$\Delta l$}
\end{pspicture}](img24.png) Corte do condutor. A normal
Corte do condutor. A normal
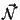 é
é
perpendicular ao papel, saindo dele.
Aplicada ao contorno da figura, e fazendo os lados paralelos à
superfície tenderem um ao outro (e à superfície), tem-se
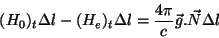 |
(12) |
onde 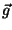 é a densidade superficial de corrente. A maneira mais
geral de se escrever esta expressão é
é a densidade superficial de corrente. A maneira mais
geral de se escrever esta expressão é
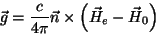 |
(13) |
onde 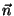 é a normal externa à superfície do condutor.
é a normal externa à superfície do condutor.
No caso em que não há correntes externas, as linhas de 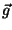 são fechadas, e aparece um momento magnético no condutor, devido
a elas. Para o caso de um condutor cilíndrico longo em um campo
uniforme
são fechadas, e aparece um momento magnético no condutor, devido
a elas. Para o caso de um condutor cilíndrico longo em um campo
uniforme 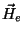 paralelo ao eixo do cilindro,
paralelo ao eixo do cilindro,
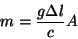 |
(14) |
onde 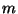 é o momento de dipolo de um trecho
é o momento de dipolo de um trecho 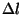 do cilindro.
O momento de dipolo por unidade de volume é a magnetização ,
que é, então, dada por
do cilindro.
O momento de dipolo por unidade de volume é a magnetização ,
que é, então, dada por
ou, em forma vetorial,
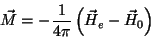 |
(17) |
Subsections



Next: Histerese no modelo de
Up: Primeiras teorias
Previous: Primeiras teorias
Henrique Fleming
2002-04-15
![]() , o que é bem verificado
experimentalmente.
, o que é bem verificado
experimentalmente.
![]() Este resultado mostra que, quando
o material se torna supercondutor, o campo magnético em seu interior é
``congelado'' no valor
Este resultado mostra que, quando
o material se torna supercondutor, o campo magnético em seu interior é
``congelado'' no valor ![]() . Alterando-se o campo magnético
externo (sem atingir o campo crítico), aparecerão então
correntes superficiais que impedirão que o campo no interior se altere.
Note-se que, como
. Alterando-se o campo magnético
externo (sem atingir o campo crítico), aparecerão então
correntes superficiais que impedirão que o campo no interior se altere.
Note-se que, como
(6,0)(6,2)(0,2)(0,0)
\psl...
...}
\uput[0](4.2,0.7){$\vec{H}_{0}$}
\uput[0](2.7,1.3){$\Delta l$}
\end{pspicture}](img24.png)
![]() são fechadas, e aparece um momento magnético no condutor, devido
a elas. Para o caso de um condutor cilíndrico longo em um campo
uniforme
são fechadas, e aparece um momento magnético no condutor, devido
a elas. Para o caso de um condutor cilíndrico longo em um campo
uniforme ![]() paralelo ao eixo do cilindro,
paralelo ao eixo do cilindro,