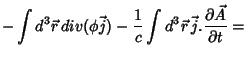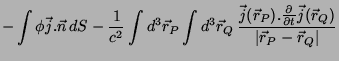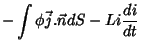Next: Resolvendo a equação
Up: Circuitos RL
Previous: Circuitos RL
Aplicando-se uma diferença de potential a um condutor
ôhmico, e supondo que a dependência temporal não seja
muito forte (freqüências da ordem de 60Hz, por exemplo),
procura-se a relação entre a força eletromotriz e a corrente.
Vamos resolver este problema, seguindo Pauli, usando
considerações energéticas. O gerador de f.e.m. é um
dispositivo qualquer, freqüentemente de natureza não
eletromagnética (por exemplo, química, no caso de
baterias), que mantém uma diferença de potencial
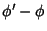 entre os extremos de um condutor ôhmico.
entre os extremos de um condutor ôhmico.
{$\phi$}
\uput[0](6.8,1.4){$\phi'$}
\end{pspicture}](img2.png) Fig.1 - Esquema do condutor
Fig.1 - Esquema do condutor
Precisaremos do importante resultado
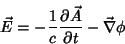 |
(1) |
que se obtém assim:
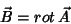 |
(2) |
e
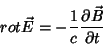 |
(3) |
Usando a Eq. 2 na Eq. 3 e utilizando a
linearidade do operador 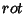 ,
podemos escrever
,
podemos escrever
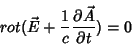 |
(4) |
Já sabemos que , para qualquer campo vetorial 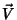 ,
a relação
,
a relação
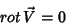 |
(5) |
implica na existência de um escalar 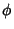 tal que
tal que
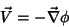 |
(6) |
Logo, usando a Eq. 5 e a Eq. 6
na Eq. 4, obtemos a Eq. 1.
No condutor considerado, a potência dissipada é dada por
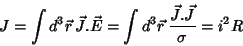 |
(7) |
onde 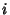 é a corrente e
é a corrente e 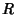 a resistência do condutor.
a resistência do condutor.
Por outro lado, usando a Eq. 1,
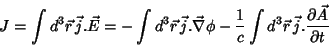 |
(8) |
Ora,
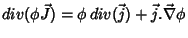 ,
e, na ausência de capacitores, podemos supor que
não haja variação de carga em nenhum ponto do circuito, ou
seja, que
,
e, na ausência de capacitores, podemos supor que
não haja variação de carga em nenhum ponto do circuito, ou
seja, que
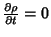 , ou, equivalentemente
(por causa da equação da continuidade), que
, ou, equivalentemente
(por causa da equação da continuidade), que 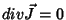 . Logo,
. Logo,
onde S é, naturalmente, a superfície externa do condutor. A
integração na superfície é simples, pois
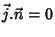 nas superfícies laterais (senão ``escaparia'' corrente pelos
lados do condutor), mas não nas ``bases'' do
condutor. Temos
nas superfícies laterais (senão ``escaparia'' corrente pelos
lados do condutor), mas não nas ``bases'' do
condutor. Temos
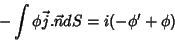 |
(10) |
Logo,
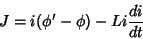 |
(11) |
Comparando com (7), obtemos
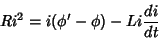 |
(12) |
Ora, 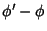 é a diferença de potencial
é a diferença de potencial 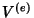 criada pela fonte de força eletromotriz (gerador). Tem-se,
então,
criada pela fonte de força eletromotriz (gerador). Tem-se,
então,
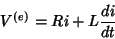 |
(13) |
que é a equação básica na ausência de capacitores.



Next: Resolvendo a equação
Up: Circuitos RL
Previous: Circuitos RL
Henrique Fleming
2001-11-29