


Next: Resolvendo a equação
Up: Circuitos RLC
Previous: Circuitos RLC
Estamos agora em condições de incluir um capacitor entre os
componentes
do nosso circuito. Idealmente, então, o circuito conterá uma
resistência
(R), uma indutância (L), e uma capacitância (C). Daí o nome RLC.
Em
relação ao caso anterior (RL), a diferença fundamental é que,
por
causa da presença do capacitor, a corrente não será mais
estacionária.
De fato, quando o capacitor estiver se carregando (ou descarregando),
haverá
uma variação de carga em suas placas. Logo, alí,
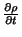 não será nula. Ora, pela
equação
da continuidade,
não será nula. Ora, pela
equação
da continuidade,
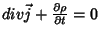 , logo,
, logo,
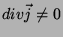 nas placas do capacitor. (Note que, porém,
nas placas do capacitor. (Note que, porém,
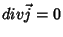 nas outras partes do circuito, pois não há acúmulo de cargas a
não
ser
nas placas do capacitor).
nas outras partes do circuito, pois não há acúmulo de cargas a
não
ser
nas placas do capacitor).
Fig.2 - Esboço de um circuito RLC
Como no caso anterior, vamos calcular a potência dissipada pelo
circuito de duas
maneiras diferentes. A primeira, idêntica ao caso anterior, dá:
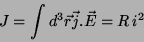 |
(23) |
enquanto que, na segunda, escrevemos 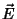 em termos dos potenciais,
obtendo
em termos dos potenciais,
obtendo
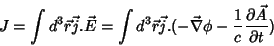 |
(24) |
A integração é estendida ao volume do condutor. Como 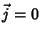 entre as
placas do capacitor, podemos dividir o volume em dois:
entre as
placas do capacitor, podemos dividir o volume em dois: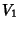 , que é o
volume do
primeiro trecho do condutor, começando na base de potencial
, que é o
volume do
primeiro trecho do condutor, começando na base de potencial 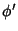 e
terminando
na primeira placa do capacitor, e
e
terminando
na primeira placa do capacitor, e 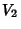 , que começa na segunda placa
e vai até
a base com potencial
, que começa na segunda placa
e vai até
a base com potencial 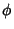 .Esses volumes são, portanto, disjuntos.
Sejam
.Esses volumes são, portanto, disjuntos.
Sejam 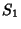 e
e
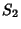 as superfícies que os delimitam.
Considere a integral
as superfícies que os delimitam.
Considere a integral
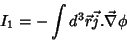 |
(25) |
que pode ser escrita como
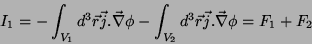 |
(26) |
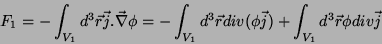 |
(27) |
Mas no interior do volume, 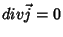 . A última integral se reduz
então
à sua contribuição na placa, que é
. A última integral se reduz
então
à sua contribuição na placa, que é
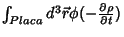 Usando
o teorema do divergente na primeira, temos:
Usando
o teorema do divergente na primeira, temos:
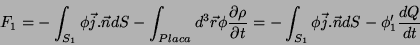 |
(28) |
Como já vimos no caso em que não havia capacitores, 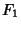 dá:
dá:
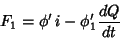 |
(29) |
É uma brincadeira de criança mostrar que, analogamente,
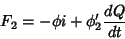 |
(30) |
Para completar o cálculo de 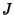 na Eq. 24 resta calcular:
na Eq. 24 resta calcular:
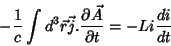 |
(31) |
já que se trata de uma repetição exata do caso RL. Temos,
portanto,
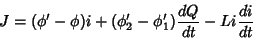 |
(32) |
Comparando (32) com (23), obtemos
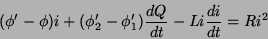 |
(33) |
de onde sai
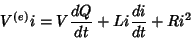 |
(34) |
onde pusemos
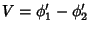 . que é a diferença de potencial
entre as placas do capacitor.
. que é a diferença de potencial
entre as placas do capacitor.
Resta determinar a relação entre 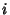 e
e 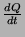 . Para
isso,
toma-se uma superfície fechada
. Para
isso,
toma-se uma superfície fechada 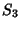 (ver Fig.2). Seja
(ver Fig.2). Seja 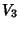 o volume delimitado por essa superfície. Temos
o volume delimitado por essa superfície. Temos
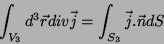 |
(35) |
que dá, pela equação da continuidade,
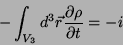 |
(36) |
ou seja,
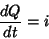 |
(37) |
Levando este resultado à Eq. 34, temos, cancelando
um fator 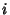 ,
,
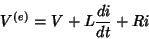 |
(38) |
Lembrando que, num capacitor, 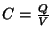 ,
,
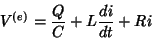 |
(39) |
Derivando mais uma vez e usando 37,
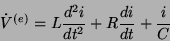 |
(40) |
que é nossa equação final.



Next: Resolvendo a equação
Up: Circuitos RLC
Previous: Circuitos RLC
Henrique Fleming
2001-11-29
{$\phi_2'$}
\uput[0](3.5,3){$+Q$}
\uput[0](4.6,3){$-Q$}
\end{pspicture}](img64.png)
{$\phi_2'$}
\uput[0](3.5,3){$+Q$}
\uput[0](4.6,3){$-Q$}
\end{pspicture}](img64.png)
![]() e
e ![]() . Para
isso,
toma-se uma superfície fechada
. Para
isso,
toma-se uma superfície fechada ![]() (ver Fig.2). Seja
(ver Fig.2). Seja ![]() o volume delimitado por essa superfície. Temos
o volume delimitado por essa superfície. Temos