


Next: Solução da homogênea
Up: Circuitos RLC
Previous: Obtendo a equação
Usando
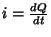 na Eq. 39 obtém-se
na Eq. 39 obtém-se
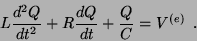 |
(41) |
Considere a equação de movimento de um oscilador harmônico
amortecido por um termo proporcional à velocidade e forçado
por uma força externa 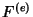 :
:
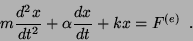 |
(42) |
As equações são idênticas, 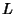 fazendo o papel da massa
(inércia),
fazendo o papel da massa
(inércia), 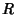 o papel de
o papel de 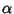 (notar que
(notar que 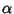 deve ser
positiva!),
deve ser
positiva!), 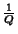 desempenhando o papel da constante
elástica
desempenhando o papel da constante
elástica 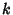 .
.
O caso mais interessante é o de uma F.E.M. periódica. Neste caso,
como no oscilador harmônico, teremos o importante fenômeno da
ressonância.
Resolve-se a Eq. 41 em duas etapas: primeiro, achamos
a solução geral da homogênea. Depois, adicionamos a ela
uma solução particular da inomogênea, obtendo a solução
geral da inomogênea.
Subsections
Henrique Fleming
2001-11-29