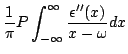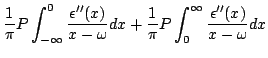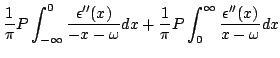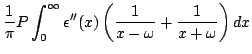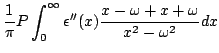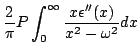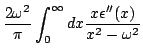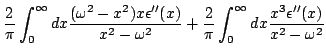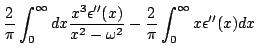Next: Relação com a velocidade
Up: Relações de dispersão
Previous: Relações de dispersão
Meios dielétricos podem ser transparentes, isto é, ter absorção
nula, para certos intervalos de freqüência. Suponhamos que um meio
seja transparente em um intervalo que inclui a freqüência 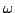 .
Então
.
Então
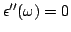 e
e
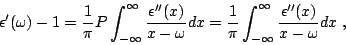 |
(36) |
já que a singularidade em 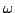 desaparece por causa do zero
no numerador. Derivando em relação a
desaparece por causa do zero
no numerador. Derivando em relação a 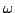 ,
,
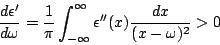 |
(37) |
ou seja, a permissividade (que nome!) cresce com a freqüência. Ora,
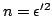 (onde
(onde 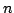 é o índice de refração), logo,
é o índice de refração), logo,
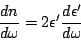 |
(38) |
Na Eq.(35), usando o fato de que
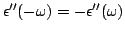 , podemos por
, podemos por
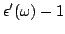 |
 |
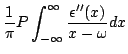 |
(39) |
| |
 |
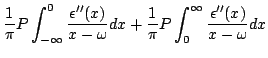 |
(40) |
| |
 |
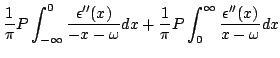 |
(41) |
| |
 |
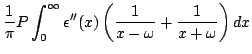 |
(42) |
| |
 |
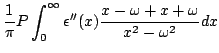 |
(43) |
| |
 |
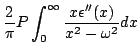 |
(44) |
Se o meio é transparente para a freqüência 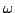 ,
,
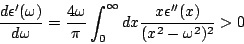 |
(45) |
de onde segue que
e
Concluíndo, temos as desigualdades
Note-se que, se 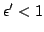 , a segunda desigualdade é mais forte.
, a segunda desigualdade é mais forte.



Next: Relação com a velocidade
Up: Relações de dispersão
Previous: Relações de dispersão
Henrique Fleming
2002-10-28