Next: Bibliography
Up: Relações de dispersão
Previous: Meios transparentes
A velocidade de propagação da onda no meio material é a velocidade de grupo,
dada por
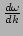 . Temos
. Temos
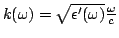 . Considere um meio não dispersivo para um certo
intervalo de freqüências que inclui
. Considere um meio não dispersivo para um certo
intervalo de freqüências que inclui 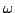 . Nele,
. Nele,
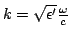 , e
, e
ou seja, a velocidade 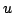 satisfaz
satisfaz
Em meios dispersivos,
Colocando 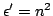 na Eq.(50), vem
na Eq.(50), vem
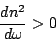 |
(51) |
de onde segue que
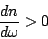 |
(52) |
que é uma relação muito importante: ela ordena as cores na dispersão. Na
decomposição da luz branca por um prisma, a luz mais desviada é o azul, de
freqüência mais alta. Note-se que não se fez uso de nenhum modelo para a
dispersão. Isto é uma conseqüência da causalidade. Note-se ainda que
Logo,
e
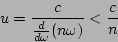 |
(53) |
que mostra que a velocidade de grupo é sempre menor que a de fase.



Next: Bibliography
Up: Relações de dispersão
Previous: Meios transparentes
Henrique Fleming
2002-10-28