


Next: About this document ...
Up: O teorema de Noether
Previous: Exemplo 2: transformações de
O campo eletromagnético livre é um campo eletromagnético na ausência de
fontes, isto é, com 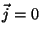 e
e 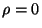 . Por exemplo, uma onda eletromagnética
se propagando numa região do espaço onde não há cargas. É descrito
pela densidade lagrangeana
. Por exemplo, uma onda eletromagnética
se propagando numa região do espaço onde não há cargas. É descrito
pela densidade lagrangeana
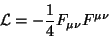 |
(43) |
com
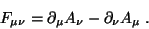 |
(44) |
No formalismo canônico as variáveis são os 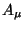 . Sob translações temos
. Sob translações temos
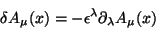 |
(45) |
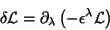 |
(46) |
e a corrente de Noether então é
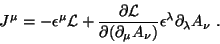 |
(47) |
Como
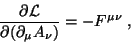 |
(48) |
podemos escrever
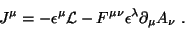 |
(49) |
A lei de conservação
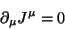 |
(50) |
pode ser escrita
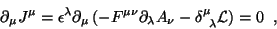 |
(51) |
e o tensor
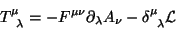 |
(52) |
é o tensor de momento-energia canônico. Há três comentários a fazer:
(i)O tensor não é independente de gauge. De fato, sob a transformação de gauge
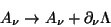 |
(53) |
temos
onde usamos as equções de Maxwell
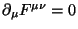 e a antissimetria
de
e a antissimetria
de 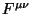 contraída com a simetria de
contraída com a simetria de
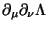 .
Não só
.
Não só
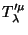 satisfaz a mesma equação de continuidade que
satisfaz a mesma equação de continuidade que
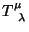 : as quantidades conservadas são também as mesmas.
: as quantidades conservadas são também as mesmas.
onde usamos de novo as equações de Maxwell (
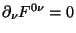 ).
).
(ii)O tensor não é simétrico, i.é,
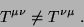 |
(59) |
Embora isto não seja crucial, põe problemas para a teoria de Einstein da gravitação,
onde o segundo membro da euqção fundamental é o tensor de momento-energia, e o
primeiro termo é simétrico. A ausência de simetria é ainda indesejável porque a expressão
para o momento angular, em termos do momento linear, não fica tão elegante. Mas é assim que
a natureza é! Suponha que 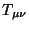 fosse sempre simétrico. Então,
fosse sempre simétrico. Então,
e a conservação do momento linear implicaria sempre na conservação do momento
angular, o que não pode ser, já que são associadas a transformações por
parâmetros independentes.
(iii)É costume trabalhar com um tensor de momento-energia modificado
(mas equivalente, no sentido de que os momentos
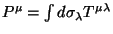 são os mesmos) e simétrico, chamado de tensor de
Belinfante-Rosenfeld.
Retomamos a relação
são os mesmos) e simétrico, chamado de tensor de
Belinfante-Rosenfeld.
Retomamos a relação
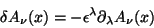 |
(61) |
e somamos a ela, e subtrímos,
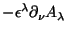 . Temos
. Temos
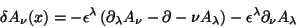 |
(62) |
Usando esta expressão na corrente de Noether, tem-se
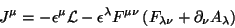 |
(63) |
e a lei de conservação é
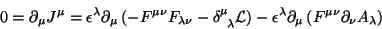 |
(64) |
Mas, no último termo,
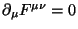 (Maxwell) e
(Maxwell) e
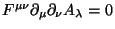 (simetria). Logo,
(simetria). Logo,
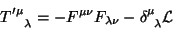 |
(65) |
satisfaz
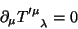 |
(66) |
bem como
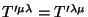 . Tem-se ainda que
. Tem-se ainda que
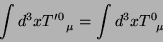 |
(67) |
É este
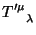 que é denominado tensor de Belinfante-
Rosenfeld.
que é denominado tensor de Belinfante-
Rosenfeld.



Next: About this document ...
Up: O teorema de Noether
Previous: Exemplo 2: transformações de
Henrique Fleming
2002-09-06
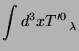
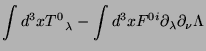
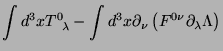
![]() são os mesmos) e simétrico, chamado de tensor de
Belinfante-Rosenfeld.
Retomamos a relação
são os mesmos) e simétrico, chamado de tensor de
Belinfante-Rosenfeld.
Retomamos a relação