


Next: Exemplo 3: Eletromagnetismo
Up: O teorema de Noether
Previous: Exemplo 1: translações
As transformações infinitesimais de Lorentz
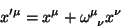 |
(27) |
com
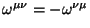 constantes, são um caso particular
das transformações infinitesimais gerais
constantes, são um caso particular
das transformações infinitesimais gerais
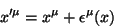 |
(28) |
onde
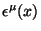 é um campo vetorial infinitesimal. Para um escalar, temos
é um campo vetorial infinitesimal. Para um escalar, temos
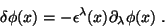 |
(29) |
Supondo que
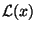 seja um escalar sob essas transformações, temos
ainda
seja um escalar sob essas transformações, temos
ainda
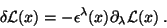 |
(30) |
Para transformações de Lorentz temos, respectivamente,
Como
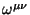 é antissimétrio, temos
é antissimétrio, temos
e então
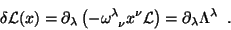 |
(36) |
A equação de continuidade de Noether então é:
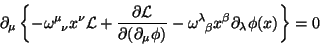 |
(37) |
que pode ser escrita
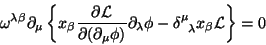 |
(38) |
ou
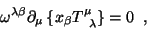 |
(39) |
onde
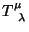 é o tensor de momento-energia canônico. Mas os
é o tensor de momento-energia canônico. Mas os
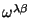 não são inteiramente arbitrários, já que são
antissimétricos. Então, da euqção acima, segue apenas que a parte antissimétrica
do termo em colchete (antissimétrica em
não são inteiramente arbitrários, já que são
antissimétricos. Então, da euqção acima, segue apenas que a parte antissimétrica
do termo em colchete (antissimétrica em
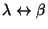 ) é nula.
Logo,
) é nula.
Logo,
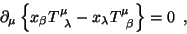 |
(40) |
que usualmente é escrita
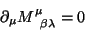 |
(41) |
onde
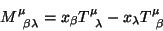 |
(42) |
é o tensor de momento angular.



Next: Exemplo 3: Eletromagnetismo
Up: O teorema de Noether
Previous: Exemplo 1: translações
Henrique Fleming
2002-09-06