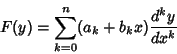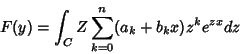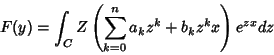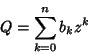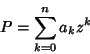Next: O Oscilador Harmônico
Up: O Famoso Apêndice de
Previous: O Famoso Apêndice de
Laplace, após ter inventado a transformação que leva o seu
nome1, generalizou-a de
várias formas. A que
nos interessa aqui, uma generalização para o plano complexo, serve para
resolver certas equações diferenciais ordinárias
muito comuns nas aplicações. São equações da forma
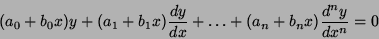 |
(1) |
que vamos também, de forma abreviada, denotar por
Vamos procurar soluções da forma
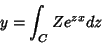 |
(2) |
onde 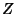 é uma função de
é uma função de 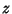 a determinar, e o contorno
a determinar, e o contorno 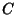 , independente
de
, independente
de 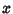 , também deve ser determinado. Como veremos, a determinação do
contorno é parte essencial na construção da solução, e aqui está talvez
a principal inovação dessa ``transformada de Laplace'' complexa.
Note-se que
, também deve ser determinado. Como veremos, a determinação do
contorno é parte essencial na construção da solução, e aqui está talvez
a principal inovação dessa ``transformada de Laplace'' complexa.
Note-se que
Como
temos,
ou
ou
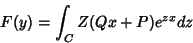 |
(3) |
com
e
Podemos então escrever 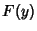 como uma soma de duas integrais:
como uma soma de duas integrais:
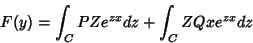 |
(4) |
A segunda dessas integrais pode ser escrita assim:
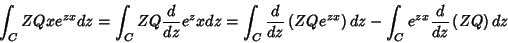 |
(5) |
Podemos agora escolher o contorno 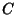 de tal sorte que a primeira integral
do segundo membro se anule. De fato, trata-se da integral de uma derivada;
logo, o valor da integral 'e a diferença dos valores do integrando nos dois
extremos. Escolhemos o contorno, então, ou como um contorno fechado, ou como
um contorno aberto em cujos dois extremos a função
de tal sorte que a primeira integral
do segundo membro se anule. De fato, trata-se da integral de uma derivada;
logo, o valor da integral 'e a diferença dos valores do integrando nos dois
extremos. Escolhemos o contorno, então, ou como um contorno fechado, ou como
um contorno aberto em cujos dois extremos a função
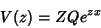 |
(6) |
tenha o mesmo valor (No caso do contorno fechado isto acontece
automaticamente). Com essa escolha de contorno,
Obtemos assim para a função 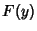 a expressão:
a expressão:
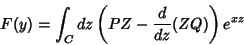 |
(7) |
Queremos determinar 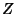 de tal forma que
de tal forma que 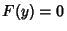 . Para tanto, o integrando
da Eq.(7) deve se anular. Assim,
. Para tanto, o integrando
da Eq.(7) deve se anular. Assim,
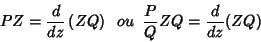 |
(8) |
o que nos leva à equação diferencial
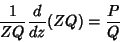 |
(9) |
Equivalentemente,
e
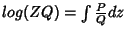 , ou ainda,
, ou ainda,
e, finalmente,
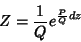 |
(10) |
A solução procurada é então
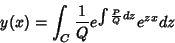 |
(11) |
ou, para maior clareza,
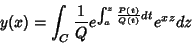 |
(12) |
onde 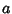 é, por exemplo, um dos zeros de
é, por exemplo, um dos zeros de 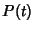 .
.



Next: O Oscilador Harmônico
Up: O Famoso Apêndice de
Previous: O Famoso Apêndice de
Henrique Fleming
2001-11-22