


Next: O Campo Uniforme
Up: O Famoso Apêndice de
Previous: A equação de Laplace
Considere a equação
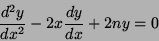 |
(13) |
que aparece na solução do problema de determinar os estados
estacionários do oscilador harmônico. Aqui 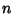 é um número qualquer,
não necessariamente um inteiro, apesar da notação. Colocando-a na forma
é um número qualquer,
não necessariamente um inteiro, apesar da notação. Colocando-a na forma
vemos que
Temos, então,
e
e, como
Logo,
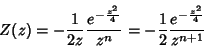 |
(14) |
e
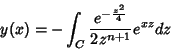 |
(15) |
Como estamos calculando uma função de onda, constantes multiplicativas
não têm importância. Por isso, simplificamos para
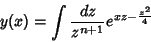 |
(16) |
Passemos agora à determinação do caminho de integração. Como vimos,
ele deve ser tal que a função 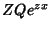 tenha o mesmo valor nos
dois extremos. Essa função é, neste caso,
tenha o mesmo valor nos
dois extremos. Essa função é, neste caso,
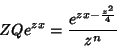 |
(17) |
Por argumentos físicos os casos de interesse
são restritos a
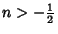 (Veja nota2). Para esses valores os contornos
(Veja nota2). Para esses valores os contornos
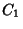 e
e 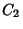 das figuras abaixo são adequados.
Seja
das figuras abaixo são adequados.
Seja 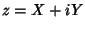 . O termo dominante no integrando é
. O termo dominante no integrando é
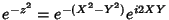 . Para
. Para 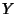 pequeno em módulo,
pequeno em módulo, 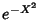 garante
que a função
garante
que a função 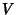 se anula nas extremidades de ambos os contornos.
Se
se anula nas extremidades de ambos os contornos.
Se 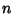 for um racional não inteiro, a origem
for um racional não inteiro, a origem 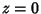 será um ponto de
ramificação, e haverá cortes ao longo do eixo real. Se o corte for
tomado ao longo do semi-eixo real negativo, o primeiro contorno não é
permitido (a curva atravessa o corte). O segundo é aceitável. A
integração é complicada, e não garante que
será um ponto de
ramificação, e haverá cortes ao longo do eixo real. Se o corte for
tomado ao longo do semi-eixo real negativo, o primeiro contorno não é
permitido (a curva atravessa o corte). O segundo é aceitável. A
integração é complicada, e não garante que 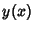 seja um polinômio,
como é requerido. Quando
seja um polinômio,
como é requerido. Quando 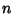 for inteiro, a situação é muito mais simples.
Façamos, neste caso, a mudança de variável
for inteiro, a situação é muito mais simples.
Façamos, neste caso, a mudança de variável
onde introduzimos a nova variável complexa 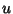 . Uma substituição simples
mostra que
. Uma substituição simples
mostra que
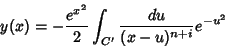 |
(18) |
onde o novo contorno 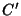 é descrito na figura abaixo.
é descrito na figura abaixo.
Que o contorno deve ser este, segue dos seguintes fatos:a transformação é
linear; uma transformação linear transforma retas em retas e círculos
em círculos3; a particular transformação acima inverte o sentido de
percurso no contorno e leva pequenos valores da parte imaginária de 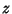 em pequenos valores da parte imaginária de
em pequenos valores da parte imaginária de 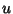 ; o ponto
; o ponto 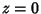 corresponde
ao ponto
corresponde
ao ponto 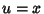 no novo contorno.
Para
no novo contorno.
Para 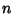 inteiro e
inteiro e 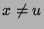 o integrando não tem singularidades. Por isso,
o contorno pode ser deformado para
o integrando não tem singularidades. Por isso,
o contorno pode ser deformado para
A integral é, então,
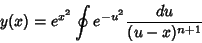 |
(19) |
Ora,
onde usamos a fórmula de Cauchy. Portanto,
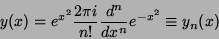 |
(20) |
Mas, uma maneira de definir os polinômios de Hermite é:
Logo,
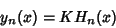 |
(21) |
onde 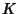 é uma constante arbitrária, a ser determinada posteriormente
pela normalização da função de onda.
é uma constante arbitrária, a ser determinada posteriormente
pela normalização da função de onda.



Next: O Campo Uniforme
Up: O Famoso Apêndice de
Previous: A equação de Laplace
Henrique Fleming
2001-11-22
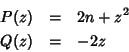
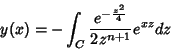
![\begin{pspicture}(0,0)(12,4)
\psline[linewidth=2pt]{->}(4.5,2.1)(3,2.1)
\pslin...
...(1,4)
\psline(0,2)(5,2)
\psline(9,0)(9,4)
\psline(6,2)(10,2)
\end{pspicture}](img51.png)