


Next: Comportamento Assintótico
Up: O Famoso Apêndice de
Previous: O Oscilador Harmônico
Nada supera em importância, na gênese da mecânica Newtoniana,
o problema da queda livre, seja da maçã, seja da Lua, em seu
movimento em redor da Terra. No entanto raramente se vê, num
curso de mecânica quântica, esses problemas tratados, nem mesmo
no caso simplificado de um campo gravitacional constante. Nesta secção
vamos resolver o problema do movimento de um ponto material sob a
ação de um campo uniforme: a queda da maçã, se a altura da queda
não for muito grande. O método de Laplace para resolver a equação
diferencial obtida será essencial.
Uma partícula de massa 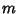 (a ``maçã'')se move sob a ação de um
campo uniforme
ao longo do eixo
(a ``maçã'')se move sob a ação de um
campo uniforme
ao longo do eixo 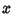 , o que lhe dá uma energia potencial
, o que lhe dá uma energia potencial
Logo, age sobre ela uma força na direção 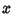 , de módulo
, de módulo 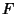 . O
movimento da partícula é também restrito (por escolha das
condições iniciais) ao eixo
. O
movimento da partícula é também restrito (por escolha das
condições iniciais) ao eixo 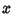 .
A equação de Schrödinger para os estados estacionários desse
sistema é:
.
A equação de Schrödinger para os estados estacionários desse
sistema é:
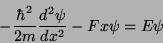 |
(22) |
ou
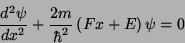 |
(23) |
É conveniente introduzir a variável adimensional
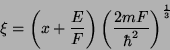 |
(24) |
Temos então
e, após algumas substituições simples,
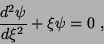 |
(25) |
como nova equação de Schrödinger.
Trata-se de uma equação de Laplace. Na notação convencional, temos
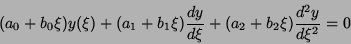 |
(26) |
à qual o método que vimos acima pode ser aplicado. Contudo, para
aproveitar os estudos prévios sobre uma função que irá aparecer
no problema (a função de Airy), vamos estudar não a equação acima,
mas uma estreitamente ligada a ela,
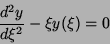 |
(27) |
que é muito conhecida na física-matemática. Se 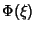 for
solução desta equação,
for
solução desta equação, 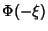 será solução da Eq.(25).
A Eq.(35) é escrita, à maneira de Laplace, assim:
será solução da Eq.(25).
A Eq.(35) é escrita, à maneira de Laplace, assim:
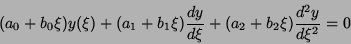 |
(28) |
com 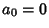 ,
, 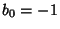 ,
, 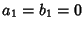 ,
, 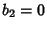 ,
, 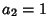 . Segue que
. Segue que
e, como
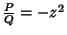 ,
,
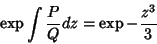 |
(29) |
e então
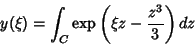 |
(30) |
Como vimos, o contorno de integração deve ser escolhido de maneira
que a função
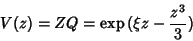 |
(31) |
tenha valores idênticos nos dois extremos. Neste caso tomaremos
um contorno que vai ao infinito, sendo os valores de 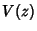 nos
dois extremos iguais a zero.
Seja
nos
dois extremos iguais a zero.
Seja 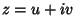 . Então
. Então
O contorno deve ser tal que a exponencial leve o integrando a zero nos
dois extremos. Para isso, devemos ter:
Consideremos primeiro o caso 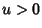 . Devemos então ter
. Devemos então ter
Esta é uma região do plano 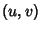 delimitada pelas retas
delimitada pelas retas
e
Na figura abaixo estão representadas essas duas retas. Sobre elas temos
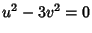 . Uma pequena reflexão com ajuda da figura convencerá o leitor
de que a região entre as retas é aquela em que
. Uma pequena reflexão com ajuda da figura convencerá o leitor
de que a região entre as retas é aquela em que 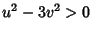 . A região
. A região
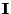 é aquela em que temos
é aquela em que temos 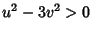 e
e 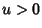 . A região simétrica
à tracejada em relação ao eixo
. A região simétrica
à tracejada em relação ao eixo 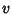 , isto é, a região
, isto é, a região
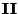 ,
é aquela em que temos
,
é aquela em que temos 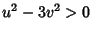 e
e
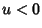 . Logo, a região em que
. Logo, a região em que 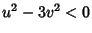 e
e 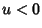 é a complementar dessa
região
é a complementar dessa
região
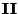 no semiplano que contém o eixo real negativo,
e é constituída pelas regiões
no semiplano que contém o eixo real negativo,
e é constituída pelas regiões
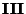 e
e
 . Essas regiões estendem-se ao infinito, embora isto
não seja (nem possa ser!) representado na figura. Em princípio o
contorno de integração pode começar em qualquer das regiões tracejadas,
e terminar em qualquer outra tracejada.
. Essas regiões estendem-se ao infinito, embora isto
não seja (nem possa ser!) representado na figura. Em princípio o
contorno de integração pode começar em qualquer das regiões tracejadas,
e terminar em qualquer outra tracejada.
Fig.1
Regiões permitidas
Na figura estão indicados, em cinza, três contornos
possíveis: 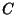 ,
, 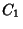 e
e 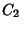 .
Desses,
.
Desses, 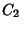 é problemático, pois se estende na região
em que a variável
é problemático, pois se estende na região
em que a variável 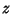 atinge valores reais e positivos. Então o termo
atinge valores reais e positivos. Então o termo
que aparece na expressão de 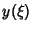 , pode, para
, pode, para 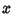 grande e positivo,
complicar a convergência da integral. Por isso tomamos os contornos
que começam na região
grande e positivo,
complicar a convergência da integral. Por isso tomamos os contornos
que começam na região
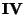 e terminam na
e terminam na
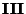 .
Em particular, o caminho
.
Em particular, o caminho 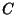 pode ser ao longo do eixo imaginário.
Então, tomando
pode ser ao longo do eixo imaginário.
Então, tomando 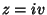 ,
,
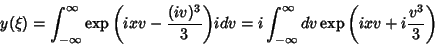 |
(32) |
ou
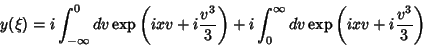 |
(33) |
ou ainda
e, finalmente,
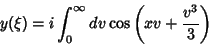 |
(34) |
A função de Airy, bem conhecida na literatura matemática,
é definida por
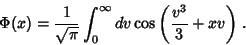 |
(35) |
Logo,
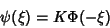 |
(36) |
Subsections



Next: Comportamento Assintótico
Up: O Famoso Apêndice de
Previous: O Oscilador Harmônico
Henrique Fleming
2001-11-22
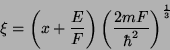
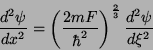
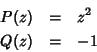
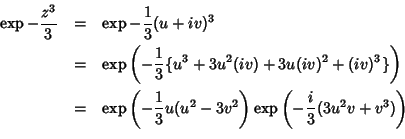
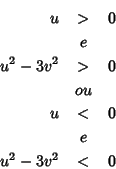
![\begin{pspicture}(0,0)(10,6)
\psline[linewidth=2pt]{->}(0,3)(10,3)
\psline[lin...
...gray]{->}(2,0)(3,1.5)(5.7,3)(9.3,4)
\uput[0](7.5,4){$\bf C_2$}
\end{pspicture}](img113.png)