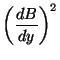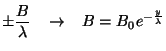Next: Demonstração geral de von
Up: Teoria de London
Previous: Teoria de London
Nesta teoria o supercondutor é considerado um condutor perfeito
(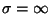 ). Neste caso a ação de um campo elétrico sobre um
elétron causa uma aceleração constante:
). Neste caso a ação de um campo elétrico sobre um
elétron causa uma aceleração constante:
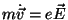 ,
e, como
,
e, como
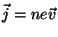 (
(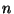 é o número de elétrons por
unidade de volume), pode-se escrever
é o número de elétrons por
unidade de volume), pode-se escrever
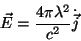 |
(29) |
onde
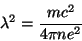 |
(30) |
Daqui segue, usando-se as equações de Maxwell, que
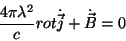 |
(31) |
Por causa da equação
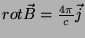 , temos
, temos
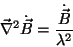 |
(32) |
Integrando no tempo segue que
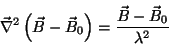 |
(33) |
onde 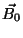 é independente do tempo.
A equação (32), como veremos a seguir, conduz a funções
é independente do tempo.
A equação (32), como veremos a seguir, conduz a funções
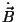 que tendem exponencialmente a zero quando se penetra
no condutor perfeito. Contudo, elas não levam ao valor
que tendem exponencialmente a zero quando se penetra
no condutor perfeito. Contudo, elas não levam ao valor 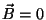 ,
e devem por isso ser modificadas. A modificação proposta por F. London
é a seguinte: um supercondutor é uma substância especial para a
qual vale a equação :
,
e devem por isso ser modificadas. A modificação proposta por F. London
é a seguinte: um supercondutor é uma substância especial para a
qual vale a equação :
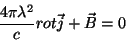 |
(34) |
Desta obtém-se, imediatamente,
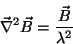 |
(35) |
ou, equivalentemente,
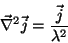 |
(36) |
Vamos examinar rapidamente esta equação .
O campo considerado tem a direção do eixo 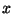 , e é tal que
, e é tal que
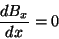 |
(37) |
A equação (35) diz que
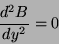 |
(38) |
![\begin{displaymath}
\frac{dB}{dy}\frac{d^2B}{dy^2}=\frac{1}{\lambda^2}B\frac{dB}...
...t[\left(\frac{dB}{dy}\right)^2-
\frac{B^2}{\lambda^2}\right]=0
\end{displaymath}](img99.png) |
(39) |
Logo, o termo entre colchetes é constante,
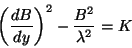 |
(40) |
Mas 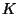 tem de ser zero, pois se sabe que, no âmago do supercondutor,
tem de ser zero, pois se sabe que, no âmago do supercondutor,
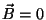 . Logo,
. Logo,
isto é, 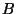 cai exponencialmente a zero, e existe um
comprimento de penetração da ordem de
cai exponencialmente a zero, e existe um
comprimento de penetração da ordem de 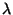
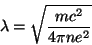 |
(43) |



Next: Demonstração geral de von
Up: Teoria de London
Previous: Teoria de London
Henrique Fleming
2002-04-15
(7,1.5)
\psline{->}(7.5...
...put[0](4,2.5){{\it Normal}}
\uput[0](4,0.5){{\it Supercondutor}}
\end{pspicture}](img95.png)
![\begin{displaymath}
\frac{dB}{dy}\frac{d^2B}{dy^2}=\frac{1}{\lambda^2}B\frac{dB}...
...t[\left(\frac{dB}{dy}\right)^2-
\frac{B^2}{\lambda^2}\right]=0
\end{displaymath}](img99.png)