


Next: Termodinâmica dos materiais magnéticos
Up: Teoria de London
Previous: Primeira versão (Becker, Heller,
A equação
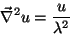 |
(44) |
é satisfeita por qualquer das componentes do campo 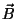 . Vamos
mostrar de uma maneira geral que ela (a equação !) descreve um amortecimento
exponencial de
. Vamos
mostrar de uma maneira geral que ela (a equação !) descreve um amortecimento
exponencial de 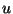 no interior de um supercondutor. Será usado o teorema
de Green
no interior de um supercondutor. Será usado o teorema
de Green
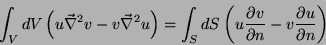 |
(45) |
Note-se que, se 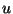 e
e 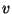 satisfazem (44), então (45)
se reduz a
satisfazem (44), então (45)
se reduz a
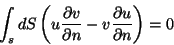 |
(46) |
A função 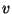 será escolhida como
será escolhida como
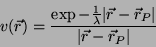 |
(47) |
que satisfaz (44) a não ser no ponto 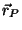 . Vamos aplicar
(46) na região interna ao supercondutor mostrado na figura.
. Vamos aplicar
(46) na região interna ao supercondutor mostrado na figura.
Em torno do ponto 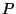 toma-se uma superfície esférica de raio
toma-se uma superfície esférica de raio 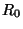 ,
e outra de raio
,
e outra de raio 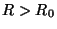 . A região considerada é a delimitada pelas duas
superfícies esféricas, mostrada em cinza na figura.
. A região considerada é a delimitada pelas duas
superfícies esféricas, mostrada em cinza na figura.
Na superfície de raio 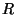 ,
,
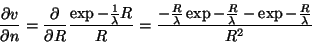 |
(48) |
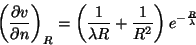 |
(49) |
e, analogamente,
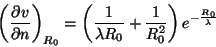 |
(50) |
Na região escolhida o teorema de Green é escrito
o que é a mesma coisa que
No limite em que a esfera de raio 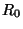 tende ao ponto, temos
tende ao ponto, temos
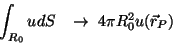 |
(53) |
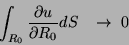 |
(54) |
Usando as eqs.(53) e (54) em (53), tem-se
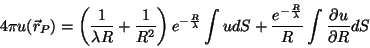 |
(55) |
Trocando-se 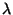 por
por 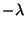 , obtém-se
, obtém-se
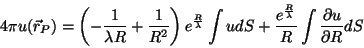 |
(56) |
Multiplicando (55) por
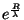 , (56) por
, (56) por
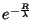 e subtraíndo, temos
e subtraíndo, temos
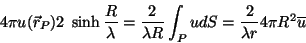 |
(57) |
ou
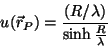 |
(58) |
Para 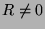 , temos
, temos
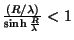 .
Logo,
.
Logo,
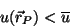 |
(59) |
Como isto é válido para qualquer esfera centrada em qualquer ponto do
supercondutor, os máximos valores de 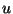 estão na superfície, e diminuem
exponencialmente com o aprofundamento no supercondutor.
Note-se que, para condutores muito pouco espessos, o fenômeno da superconutividade
é muito diferente, já que o campo magnético não chega a se anular na espessura
do condutor. Isto abriu uma área de pesquisa, dos supercondutores superficiais.
estão na superfície, e diminuem
exponencialmente com o aprofundamento no supercondutor.
Note-se que, para condutores muito pouco espessos, o fenômeno da superconutividade
é muito diferente, já que o campo magnético não chega a se anular na espessura
do condutor. Isto abriu uma área de pesquisa, dos supercondutores superficiais.



Next: Termodinâmica dos materiais magnéticos
Up: Teoria de London
Previous: Primeira versão (Becker, Heller,
Henrique Fleming
2002-04-15
![]() ,
,
![$\displaystyle \int_R dS\left[-u\left(\frac{1}{\lambda R}+\frac{1}{R^2}\right)e^...
...\lambda}}
-\frac{e^{-\frac{R}{\lambda}}}{R}\frac{\partial u}{\partial R}\right]$](img123.png)
![$\displaystyle \int_{R_{0}} dS\left[u\left(\frac{1}{\lambda R_{0}}+\frac{1}{R_{0...
...frac{e^{-\frac{R_{0}}{\lambda}}}{R_{0}}\frac{\partial u}{\partial R_{0}}\right]$](img125.png)