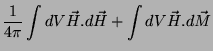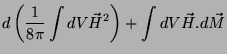Next: Transições de fase de
Up: Primeiras teorias
Previous: Demonstração geral de von
Se um pedaço de matéria sofre a ação de um campo magnético, adquire, em geral, um
momento magnético. O processo envolve energia, e é preciso incluir esta
energia na identidade termodinâmica. O trabalho magnético será da forma
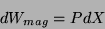 |
(60) |
e, para determinar essas quantidades, vamos usar o arranjo esboçado na figura
Um solenoide de fio supercondutor é ligado a uma bateria de força eletromotriz
regulável. Dentro do solenóide há um pedaço de matéria que será chamado
de sistema termodinâmico (ST). O solenóide se separa do ambiente
por uma parede adiabática.
Seja 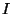 a corrente que passa no solenóide, e
a corrente que passa no solenóide, e
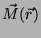 a magnetização
do
a magnetização
do  . Variando
. Variando 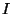 , varia
, varia
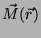 . Supõe-se que a função
. Supõe-se que a função
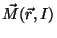 seja unívoca de
seja unívoca de 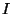 (estão excluídos, assim, os materiais
ferromagnéticos).
(estão excluídos, assim, os materiais
ferromagnéticos).
Na ausência de 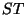 a corrente produzirá um campo
a corrente produzirá um campo
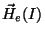 , que é uma
função determinada de
, que é uma
função determinada de 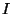 . Este campo externo pode ser uma função da posição dentro
do solenóide, e depende linearmente de
. Este campo externo pode ser uma função da posição dentro
do solenóide, e depende linearmente de 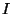 1. Logo,
1. Logo,
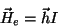 |
(61) |
onde
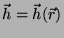 .
Aumentando-se a corrente, o campo externo
.
Aumentando-se a corrente, o campo externo 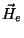 aumenta, e o momento magnético
varia, em resposta. Para isso a bateria deve fornecer trabalho, e o que procuramos é a
relação entre o trabalho feito por ela e as mudanças em
aumenta, e o momento magnético
varia, em resposta. Para isso a bateria deve fornecer trabalho, e o que procuramos é a
relação entre o trabalho feito por ela e as mudanças em 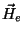 e
e
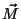 .
.
A potência gasta pela bateria é
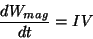 |
(62) |
onde 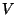 é a força eletromotriz induzida na bobina pelas variações
nos fluxos magnéticos. Provém de dois fatores:
é a força eletromotriz induzida na bobina pelas variações
nos fluxos magnéticos. Provém de dois fatores:
1. Na ausência do 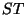 , provém da variação de
, provém da variação de 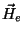 . Esta parte é,
então, dada por
. Esta parte é,
então, dada por
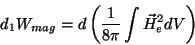 |
(63) |
2.Efeitos devidos à presença do sistema termodinâmico. Suponhamos que, no ponto
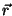 , exista uma pequena espira de área
, exista uma pequena espira de área 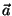 e corrente
e corrente 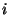 , com
um momento magnético, então, dado por
, com
um momento magnético, então, dado por
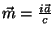 .
O campo do solenoide no ponto
.
O campo do solenoide no ponto 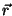 é
é
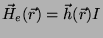 .
O fluxo deste campo na espira é
.
O fluxo deste campo na espira é
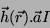 |
(64) |
Ora, o fluxo que atravessa a espira é
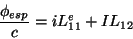 |
(65) |
(note que
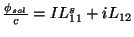 )
onde
)
onde 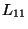 é o coeficiente de autoindução e
é o coeficiente de autoindução e 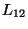 é o coeficiente
de indição mútua. Logo,
é o coeficiente
de indição mútua. Logo,
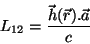 |
(66) |
Se a corrente na espira varia, a 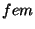 induzida no solenoide é
induzida no solenoide é
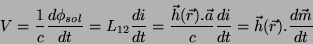 |
(67) |
ou ainda,
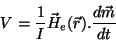 |
(68) |
e, por conseguinte, para um dipolo,
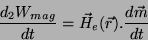 |
(69) |
Pondo
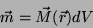 |
(70) |
tem-se
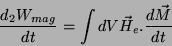 |
(71) |
Somando as duas contribuições ,
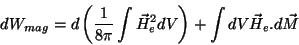 |
(72) |
Pelos nossos resultados gerais, deveríamos esperar o seguinte:
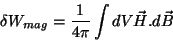 |
(73) |
e, como
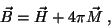 |
(74) |
onde 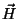 agora é o campo magnético real. Mas é claro que
agora é o campo magnético real. Mas é claro que
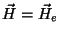 , logo, as duas quantidades coincidem.
, logo, as duas quantidades coincidem.



Next: Transições de fase de
Up: Primeiras teorias
Previous: Demonstração geral de von
Henrique Fleming
2002-04-15
(7,-1)(7,5)(-1,5)(-1,-1)
\end{pspicture}](img141.png)
![]() a corrente que passa no solenóide, e
a corrente que passa no solenóide, e
![]() a magnetização
do
a magnetização
do ![]() . Variando
. Variando ![]() , varia
, varia
![]() . Supõe-se que a função
. Supõe-se que a função
![]() seja unívoca de
seja unívoca de ![]() (estão excluídos, assim, os materiais
ferromagnéticos).
(estão excluídos, assim, os materiais
ferromagnéticos).
![]() a corrente produzirá um campo
a corrente produzirá um campo
![]() , que é uma
função determinada de
, que é uma
função determinada de ![]() . Este campo externo pode ser uma função da posição dentro
do solenóide, e depende linearmente de
. Este campo externo pode ser uma função da posição dentro
do solenóide, e depende linearmente de ![]() 1. Logo,
1. Logo,