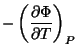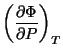Next: Teoria da supercondutividade de
Up: Supercondutividade Teorias clássicas
Previous: Transições de fase de
Considerando as grandezas termodinâmicas do cristal a um valor dado de 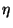 ,
podemos pensar o potencial termodinâmico como uma função de
,
podemos pensar o potencial termodinâmico como uma função de 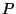 ,
,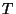 e
e 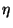 .
Contudo, na função
.
Contudo, na função
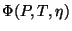 , a última variável desempenha um
papel diferente, pois, dados
, a última variável desempenha um
papel diferente, pois, dados 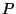 e
e 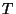 de uma maneira arbitrária,
de uma maneira arbitrária, 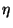 é determinada pelo fato de que deve ter o valor que minimiza o potencial
para aqueles valores de
é determinada pelo fato de que deve ter o valor que minimiza o potencial
para aqueles valores de 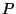 e
e 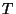 . A continuidade da variação do estado
durante uma transição de segunda ordem se exprime matematicamente pelo
fato de que, nas vizinhanças do ponto de transição ,
. A continuidade da variação do estado
durante uma transição de segunda ordem se exprime matematicamente pelo
fato de que, nas vizinhanças do ponto de transição , 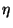 assume valores
arbitrariamente pequenos. Ali, então ,
assume valores
arbitrariamente pequenos. Ali, então ,
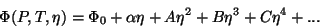 |
(77) |
Sendo os coeficientes 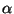 ,
, 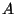 ,
, 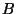 ,
, 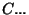 funções de
funções de 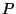 e
e 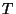 .
.
Teorema 1: se os estados com 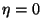 e
e 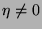 se distinguem
pela simetria, então
se distinguem
pela simetria, então 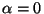 . A demonstração deste teorema é muito
longa para estas notas2.
. A demonstração deste teorema é muito
longa para estas notas2.
Teorema 2: no ponto de transição ,
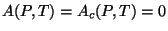 .
.
Demonstração :a) Na fase simétrica, 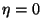 deve corresponder a um
mínimo de
deve corresponder a um
mínimo de 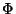 . Logo, devemos ter
. Logo, devemos ter
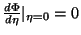 e
e
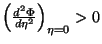 Esta última condição é
Esta última condição é
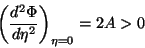 |
(78) |
b) Na fase não simétrica, 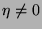 deve corresponder a um mínimo de
deve corresponder a um mínimo de
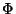 , isto é, para cada par (P,T) deve haver um mínimo de
, isto é, para cada par (P,T) deve haver um mínimo de 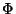 em um ponto
diferente de zero. Para que isto ocorra,
em um ponto
diferente de zero. Para que isto ocorra, 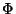 deve ter o aspecto da figura, que
é o que se obtém tomando
deve ter o aspecto da figura, que
é o que se obtém tomando 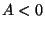 e supondo que as demais contribuições
sejam, no global, positivas.
De fato,
e supondo que as demais contribuições
sejam, no global, positivas.
De fato,
i)Suponha 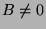 . Então , devemos ter
. Então , devemos ter
para 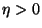 .
.
Da primeira, 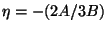 . Levando à segunda,
. Levando à segunda,
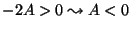 .
.
ii)Se 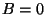 ,
,
Então , como 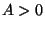 de um lado do ponto de transição e
de um lado do ponto de transição e 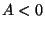 do outro,
do outro,
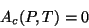 |
(83) |
Teorema 3:
Pois então , no ponto de transição ,
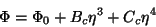 |
(86) |
Para que haja mínimo para 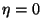 é preciso que
é preciso que
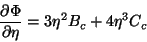 |
(87) |
mude de sinal ao passar por 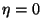 . Para isso,
. Para isso, 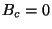 . É óbvio
que o mínimo implica
. É óbvio
que o mínimo implica 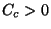 . Por continuidade,
. Por continuidade, 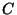 é positivo
também nas vizinhanças do ponto de transição . Há duas situações
possíveis:
é positivo
também nas vizinhanças do ponto de transição . Há duas situações
possíveis:
1)
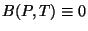 . (
. (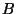 é identicamente nulo). A condição que determina
o ponto de transição é, então ,
é identicamente nulo). A condição que determina
o ponto de transição é, então ,
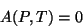 |
(88) |
e se tem uma linha de pontos de transição no plano 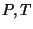 .
.
2)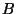 não é identicamente nulo. Há então duas equações
não é identicamente nulo. Há então duas equações
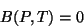 |
(89) |
e
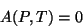 |
(90) |
Os pontos de transição são isolados.
Usaremos o nome de transições de segunda ordem apenas para o caso 1). Logo,
estaremos sempre supondo 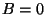 . A forma geral para
. A forma geral para 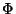 é, então ,
é, então ,
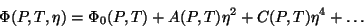 |
(91) |
sendo 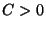 e
e
Fixando-se a pressão , examinemos 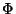 do ponto de vista da temperatura.
Nas vizinhanças do ponto de transição
do ponto de vista da temperatura.
Nas vizinhanças do ponto de transição 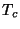 , temos
, temos
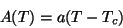 |
(95) |
Para 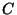 , usaremos
, usaremos
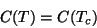 |
(96) |
Para determinar 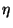 em função da temperatura, põe-se
em função da temperatura, põe-se
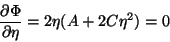 |
(97) |
que dá
Note-se que
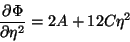 |
(100) |
Para
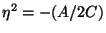 , temos
, temos
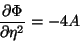 |
(101) |
Para que isto seja um mínimo, 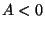 . Isto é,
. Isto é,
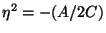 é
um estado de equilíbrio na fase em que
é
um estado de equilíbrio na fase em que 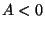 (não simétrica).
Inversamente, para
(não simétrica).
Inversamente, para 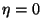 ,
,
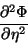 |
(102) |
mostrando que 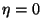 é um estado de equilíbrio para a fase na qual
é um estado de equilíbrio para a fase na qual
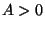 (simétrica). A solução
(simétrica). A solução 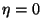 na fase não -simétrica
é um máximo do potencial termodinâmico!
na fase não -simétrica
é um máximo do potencial termodinâmico!
Para calcular a entropia usamos
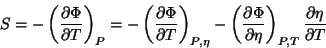 |
(103) |
e, pela condição de mínimo,
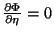 ,
logo,
,
logo,
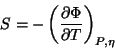 |
(104) |
Esta expressão é válida nas vizinhanças do ponto de transição .
Na fase simétrica, 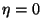 e então
e então 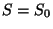 . Na fase não -simétrica,
. Na fase não -simétrica,
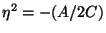 . Logo,
. Logo,
Resumindo,
logo, a entropia é contínua na transição .
De (111) se pode determinar facilmente o calor espec
i fico
a pressão constante
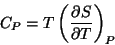 |
(112) |
obtendo
sendo
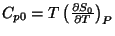 .
.
O calor específico é então descontínuo na transição . Uma
informação importante é que, como 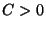 , no ponto de transição se tem
, no ponto de transição se tem
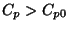 , isto é, o calor específico aumenta na passagem da fase
simétrica para a não-simétrica.
, isto é, o calor específico aumenta na passagem da fase
simétrica para a não-simétrica.
Outros saltos podem ser obtidos das relações 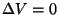 e
e  da forma seguinte: a curva de transição , dada por
da forma seguinte: a curva de transição , dada por 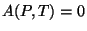 , tem
uma equação
, tem
uma equação 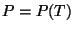 . Derivando a equação
. Derivando a equação 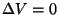 ao longo
da curva de transição em relação à temperatura, temos
ao longo
da curva de transição em relação à temperatura, temos
![\begin{displaymath}
\frac{d}{dT}\Delta V\left(P(T),T\right)=
\Delta \left[\left(...
...frac{
\partial V}{\partial P}\right)_{T}\frac{dP}{dT}\right]=0
\end{displaymath}](img268.png) |
(116) |
isto é,
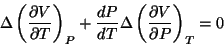 |
(117) |
Por outro lado, de  segue que
segue que
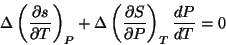 |
(118) |
Ora,
Logo,
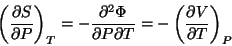 |
(121) |
e, então , de (118),
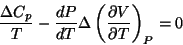 |
(122) |



Next: Teoria da supercondutividade de
Up: Supercondutividade Teorias clássicas
Previous: Transições de fase de
Henrique Fleming
2002-04-15
![]() . Levando à segunda,
. Levando à segunda,
![]() .
.
![]() ,
,
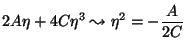
![]() . A forma geral para
. A forma geral para ![]() é, então ,
é, então ,
![]() do ponto de vista da temperatura.
Nas vizinhanças do ponto de transição
do ponto de vista da temperatura.
Nas vizinhanças do ponto de transição ![]() , temos
, temos
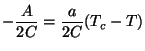
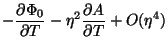
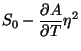
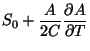
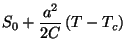
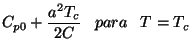
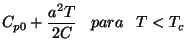
![]() , no ponto de transição se tem
, no ponto de transição se tem
![]() , isto é, o calor específico aumenta na passagem da fase
simétrica para a não-simétrica.
, isto é, o calor específico aumenta na passagem da fase
simétrica para a não-simétrica.
![]() e
e ![]() da forma seguinte: a curva de transição , dada por
da forma seguinte: a curva de transição , dada por ![]() , tem
uma equação
, tem
uma equação ![]() . Derivando a equação
. Derivando a equação ![]() ao longo
da curva de transição em relação à temperatura, temos
ao longo
da curva de transição em relação à temperatura, temos