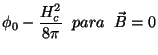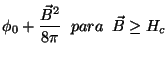Next: Argumento de Rose-Innes, Rhoderic
Up: Teoria da supercondutividade de
Previous: Teoria da supercondutividade de
Há problemas no confronto com a experiência.
1.O acordo das equções de London com a experiência é qualitativo;
quantitativamente o acordo é duvidoso.
2.A teoria está em contradição com a experiência em relação à destruição
da supercondutividade de um filme fino por um campo magnético. De fato, o uso da
termodinâmica acoplada às equações de london leva, para o caso da transição
de um filme fino de espessura 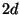 do estado supercondutor para o normal, à seguinte
expressão para o campo magnético
do estado supercondutor para o normal, à seguinte
expressão para o campo magnético 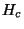 :
:
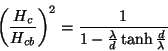 |
(123) |
onde 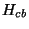 é o campo crítico de um supercondutor volumoso de mesmo material. Esta
expressão não está de acordo com a experiência, pois, medindo-se
é o campo crítico de um supercondutor volumoso de mesmo material. Esta
expressão não está de acordo com a experiência, pois, medindo-se
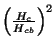 e variando-se
e variando-se 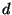 , não se obtém um valor constante
para
, não se obtém um valor constante
para 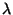 .
.
3. Questões ligadas à energia superficial.
Assim, a teoria precisa ser modificada.
O primeiro fato importante é que o campo crítico é uma função da temperatura.
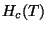 se anula à temperatura crítica, com um slope finito. As variáveis
relevantes são o campo magnético, a temperatura e a pressão . Como, porém, as
mudanças de volume no processo são muito pequenas, ignoraremos a dependência na
pressão .
se anula à temperatura crítica, com um slope finito. As variáveis
relevantes são o campo magnético, a temperatura e a pressão . Como, porém, as
mudanças de volume no processo são muito pequenas, ignoraremos a dependência na
pressão .
A variação da energia por centímetro cúbico é dada por
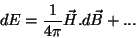 |
(124) |
Em um processo isotérmico, toda a energia magnética pode ser transformada em trabalho,
logo,
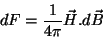 |
(125) |
Integrando,
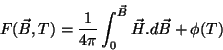 |
(126) |
sendo 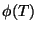 uma finção só da temperatura. É preferível trabalhar com potenciais
termodinâmicos que tenham como variável independente
uma finção só da temperatura. É preferível trabalhar com potenciais
termodinâmicos que tenham como variável independente 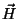 , pois, enquanto
, pois, enquanto
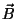 é uma função unívoca de
é uma função unívoca de 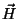 , p inverso não é verdade.
, p inverso não é verdade.
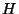 não é uma função unívoca de
não é uma função unívoca de 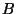 .
.
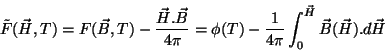 |
(127) |
onde se supõe que
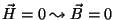 .
.
De acordo com Meissner,
e, em conseqüência ,
Como
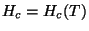 e
e
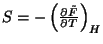 temos, para a parte normal,
temos, para a parte normal,
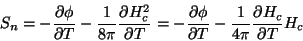 |
(132) |
e
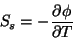 |
(133) |
para a fase supercondutora. Logo,
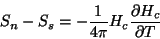 |
(134) |
o que mostra que a transição é de primeira ordem quando se dá na presença de
um campo magnético (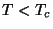 ), envolvendo um calor de transição por mol
), envolvendo um calor de transição por mol
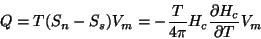 |
(135) |
que é absorvido pelo sistema quando a transição se dá do estado supercondutor para
o normal. Por outro lado, na ausência de campo magnético a transição se dá
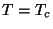 com
com
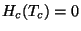 . Logo,
. Logo, 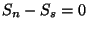 , e a transição é de segunda
ordem.
, e a transição é de segunda
ordem.
Derivando (134) e multiplicando por 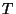 temos, para os calores específicos
por mol,
temos, para os calores específicos
por mol,
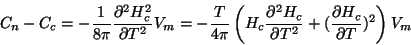 |
(136) |
e, em 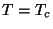 ,
,
![\begin{displaymath}
\left[C_{n}-C_{s}\right]_{T=T_{c}}=-\frac{T}{4\pi}\left(\frac{\partial H_{c}}{\partial T}
\right)^{2}_{T=T_{c}}V_{m}
\end{displaymath}](img309.png) |
(137) |
que é a fórmula de Rutgers.
Finalmente, para a energia livre 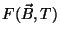 , temos, introduzindo
, temos, introduzindo
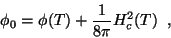 |
(138) |
Consideremos a situação em que 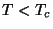 . Vamos estimar o valor da diferença
entre
. Vamos estimar o valor da diferença
entre
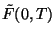 e
e
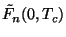 , onde esta última
é a energia livre da fase normal à temperatura
, onde esta última
é a energia livre da fase normal à temperatura 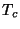 . A presença de um
campo magnético não causa praticamente nenhum efeito na fase normal. Então ,
já que a transição , com
. A presença de um
campo magnético não causa praticamente nenhum efeito na fase normal. Então ,
já que a transição , com 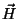 , é de primeira ordem, podemos estender
, é de primeira ordem, podemos estender
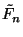 para
para 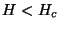 . Supomos a mesma forma, isto é:
. Supomos a mesma forma, isto é:
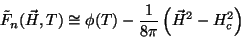 |
(141) |
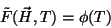 |
(142) |
Logo,
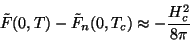 |
(143) |



Next: Argumento de Rose-Innes, Rhoderic
Up: Teoria da supercondutividade de
Previous: Teoria da supercondutividade de
Henrique Fleming
2002-04-15
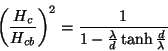
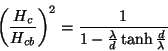
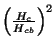 e variando-se
e variando-se {1500}
\psdots(1,0)(2,0)(3,0)(4,0)(5,0)(6,0)
\end{pspicture}](img283.png)
(4,4)
\psline[linestyle=dotted](4,1)(4,4)
\end{pspicture}](img288.png)
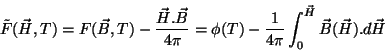
![]() temos, para os calores específicos
por mol,
temos, para os calores específicos
por mol,
![\begin{displaymath}
\left[C_{n}-C_{s}\right]_{T=T_{c}}=-\frac{T}{4\pi}\left(\frac{\partial H_{c}}{\partial T}
\right)^{2}_{T=T_{c}}V_{m}
\end{displaymath}](img309.png)
![]() , temos, introduzindo
, temos, introduzindo