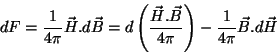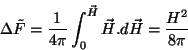Next: Teoria de Ginzburg-Landau
Up: Teoria da supercondutividade de
Previous: Problemas com a teoria
Considere um supercondutor com a forma de um longo bastão. Quando ele é resfriado
a uma temperatura 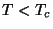 , torna-se supercondutor. Isto quer dizer que, pata
, torna-se supercondutor. Isto quer dizer que, pata 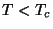 os
potenciais termodinâmicos da fase supercondutora têm um valor menor do que os análogos
da fase normal (se não, o material permaneceria na fase normal). Suponhamos que a essa
temperatura e na ausência de campo magnético externo (
os
potenciais termodinâmicos da fase supercondutora têm um valor menor do que os análogos
da fase normal (se não, o material permaneceria na fase normal). Suponhamos que a essa
temperatura e na ausência de campo magnético externo (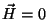 ) a energia livre
por unidade de volume no estado supercondutor seja
) a energia livre
por unidade de volume no estado supercondutor seja 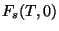 , e na fase normal seja
, e na fase normal seja
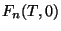 .
.
Suponhamos agora que um campo magnético seja ligado paralelamente ao bastão , e vejamos
como vão variar os potenciais termodinâmicos. A energia livre de todo o sistema
é aumentada de
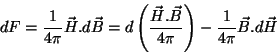 |
(144) |
Definindo o novo potencial termodinâmico 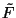 , temos
, temos
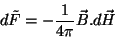 |
(145) |
Queremos isolar nesta expressão o termo que corresponde à mudança da energia livre do bastão
supercondutor. O processo físico responsável por isto é a magnetização
do bastão .
Como se tem
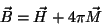 |
(146) |
pomos
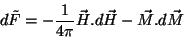 |
(147) |
de onde se vê que a variação correspondente ao supercondutor é
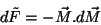 |
(148) |
Mas, no supercondutor,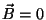 , logo,
, logo,
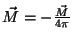 . Logo,
. Logo,
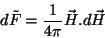 |
(149) |
O aumento de energia livre, uma vez aplicado o campo, é, então ,
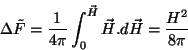 |
(150) |
isto é
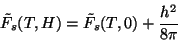 |
(151) |
Logo, a aplicação de um campo externo aumenta a energia livre da fase supercondutora.
A condição para que o material se mantenha supercondutor é que
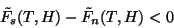 |
(152) |
e, como
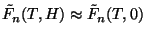 ,
,
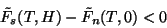 |
(153) |
o que dá, ainda,
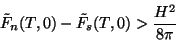 |
(154) |
O campo crítico é aquele para o qual
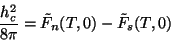 |
(155) |
Uma expressão útil para o campo crítico é obtida supondo-se que
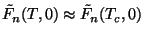 . Então ,
. Então ,
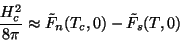 |
(156) |



Next: Teoria de Ginzburg-Landau
Up: Teoria da supercondutividade de
Previous: Problemas com a teoria
Henrique Fleming
2002-04-15
$}
\uput[0](7.5,4){$F_{s}(T,H)$}
\uput[0](2.5,3.2){$Normal$}
\end{pspicture}](img325.png)
$}
\uput[0](7.5,4){$F_{s}(T,H)$}
\uput[0](2.5,3.2){$Normal$}
\end{pspicture}](img325.png)