


Next: Transformações das componentes de
Up: Introdução aos tensores
Previous: Introdução aos tensores
Sejam 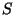 ({
({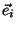 }) e
}) e 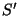 ({
({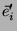 }) duas bases ortonormais
do espaço usual (
}) duas bases ortonormais
do espaço usual (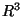 como espaço vetorial, com o produto escalar
usual). Cada vetor de
como espaço vetorial, com o produto escalar
usual). Cada vetor de 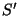 pode ser expandido na base
pode ser expandido na base 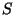 . Denotamos essa
expansão assim:
. Denotamos essa
expansão assim:
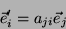 |
(1) |
Naturalmente temos, também, a expansão
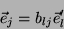 |
(2) |
Combinando as duas, obtemos
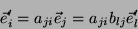 |
(3) |
de onde segue que
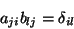 |
(4) |
Seja 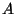 a matriz tal que
a matriz tal que 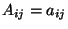 e
e 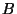 tal que
tal que 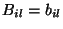 .
Então a equação anterior se escreve
.
Então a equação anterior se escreve
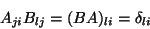 |
(5) |
Analogamente,
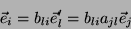 |
(6) |
Logo,
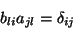 |
(7) |
ou
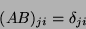 |
(8) |
Isto mostra que 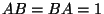 , ou seja, que as matrizes
, ou seja, que as matrizes 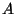 e
e 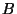 são inversas.
são inversas.
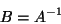 |
(9) |
Subsections



Next: Transformações das componentes de
Up: Introdução aos tensores
Previous: Introdução aos tensores
Henrique Fleming
2002-04-15