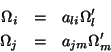Next: Eixos não ortogonais
Up: Mudanças de base
Previous: Transformações das componentes de
Considere um corpo rígido: um sistema de partículas cujas distâncias
de umas as outras permanecem fixas. Seja 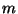 a massa de uma
partícula genérica, e
a massa de uma
partícula genérica, e 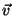 a sua velocidade. O momento total do corpo
rígido será então
a sua velocidade. O momento total do corpo
rígido será então
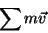 |
(20) |
A notação usual seria: 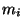 é a massa da i-ésima partícula,
é a massa da i-ésima partícula,
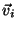 sua velocidade, e o momento total,
sua velocidade, e o momento total,
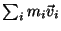 .
Contudo, queremos economizar índices, por isso omitimos aquele que
identificaria cada partícula. A convenção é esta: uma letra
minúscula representa quantidades de uma partícula; letras
maiúsculas representam quantidades comuns a todas as partículas.
Um resultado fundamental da mecânica é que a velocidade
instantânea de cada ponto do corpo rígido,
.
Contudo, queremos economizar índices, por isso omitimos aquele que
identificaria cada partícula. A convenção é esta: uma letra
minúscula representa quantidades de uma partícula; letras
maiúsculas representam quantidades comuns a todas as partículas.
Um resultado fundamental da mecânica é que a velocidade
instantânea de cada ponto do corpo rígido, 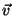 , pode
ser decomposta assim:
, pode
ser decomposta assim:
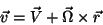 |
(21) |
onde 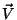 é uma velocidade comum a todas as partículas,
e
é uma velocidade comum a todas as partículas,
e 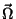 é a velocidade angular instantânea (
também a mesma para todas as partículas). Naturalmente,
é a velocidade angular instantânea (
também a mesma para todas as partículas). Naturalmente, 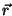 é o vetor de posição de cada partícula.1
A energia cinética do corpo rígido pode então ser escrita:
é o vetor de posição de cada partícula.1
A energia cinética do corpo rígido pode então ser escrita:
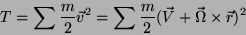 |
(22) |
onde, como é usual, o quadrado de um vetor é o produto
escalar dele consigo mesmo. Calculando este produto escalar,
obtemos
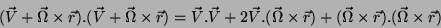 |
(23) |
O segundo termo do segundo membro aparece, na energia cinética,
sob a forma
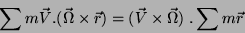 |
(24) |
Mas o termo 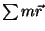 pode ser posto igual a zero, se tomarmos
a origem no centro de massa do corpo. De fato, sejam
pode ser posto igual a zero, se tomarmos
a origem no centro de massa do corpo. De fato, sejam 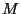 a massa total
do corpo, e
a massa total
do corpo, e 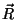 a posição de seu centro de massa. Então
a posição de seu centro de massa. Então
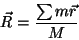 |
(25) |
e, se o centro de massa está na origem, 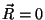 , o mesmo
valendo, então, para
, o mesmo
valendo, então, para 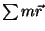 . A energia cinética é
então escrita
. A energia cinética é
então escrita
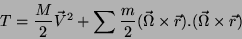 |
(26) |
O último termo pode ser reescrito assim:
o que dá, para a energia cinética,
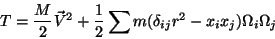 |
(32) |
e, se definirmos as componentes do momento de inércia como
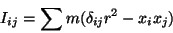 |
(33) |
teremos
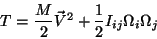 |
(34) |
O momento de inércia é construído com as componentes do
vetor 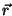 , mas não é um vetor. Suas componentes
contêm produtos das componentes de
, mas não é um vetor. Suas componentes
contêm produtos das componentes de 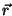 . Uma quantidade desse
tipo é dita um tensor. Fala-se, então, no tensor momento
de inércia. Vamos obter agora a maneira pela qual as componentes do
tensor momento de inérica se transformam por mudança de base.
A energia cinética é um invariante, pois não é alterada
por uma mudança de base. Ora, a quantidade
. Uma quantidade desse
tipo é dita um tensor. Fala-se, então, no tensor momento
de inércia. Vamos obter agora a maneira pela qual as componentes do
tensor momento de inérica se transformam por mudança de base.
A energia cinética é um invariante, pois não é alterada
por uma mudança de base. Ora, a quantidade
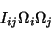 |
(35) |
comparece na expressão da energia cinética, sendo, também,
um invariante. Logo, se mudarmos de base, teremos
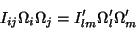 |
(36) |
onde as quantidades do segundo membro são componentes em relação à
segunda base. As propriedades de transformação das componentes de
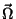 são conhecidas, pois trata-se de um vetor.
Então,
são conhecidas, pois trata-se de um vetor.
Então,
que, levadas à Eq.(36), dão
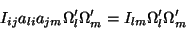 |
(37) |
Comparando, segue que
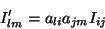 |
(38) |
que dá a fórmula de transformação das componentes do
tensor de inércia por mudança de base. Inspirados nesse resultado,
definimos: tensor de segunda ordem é um conjunto de
pares (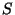 ,
, 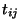 ), onde
), onde 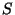 é uma base e
é uma base e 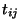 são
números, sendo que esses números se relacionam aos de outra
base pelas relações (ditas fórmulas de transformação )
são
números, sendo que esses números se relacionam aos de outra
base pelas relações (ditas fórmulas de transformação )
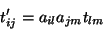 |
(39) |
sendo os 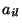 os mesmos coeficientes que aparecem na
fórmula de transformação das componentes de um vetor. Isto
permite que se diga que um tensor de segunda ordem transforma-se
como o produto de dois vetores.
Chegamos às propriedades de transformação do tensor de
inércia a partir do fato de que
os mesmos coeficientes que aparecem na
fórmula de transformação das componentes de um vetor. Isto
permite que se diga que um tensor de segunda ordem transforma-se
como o produto de dois vetores.
Chegamos às propriedades de transformação do tensor de
inércia a partir do fato de que 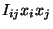 devia ser
um invariante. Vejamos agora um outro tensor que pode ser
descoberto dessa forma: sejam
devia ser
um invariante. Vejamos agora um outro tensor que pode ser
descoberto dessa forma: sejam 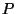 , de coordenadas
, de coordenadas 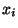 e
e
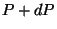 , de coordenadas
, de coordenadas 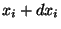 dois pontos muito
próximos. O quadrado da distância entre eles é dado
em termos das coordenadas por
dois pontos muito
próximos. O quadrado da distância entre eles é dado
em termos das coordenadas por
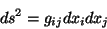 |
(40) |
onde 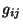 são coeficientes que dependem da base
considerada. Como
são coeficientes que dependem da base
considerada. Como 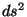 é um invariante (a distância
entre dois pontos não depende da base considerada)
concluímos, pela mesma seqüência de argumentos, que
é um invariante (a distância
entre dois pontos não depende da base considerada)
concluímos, pela mesma seqüência de argumentos, que
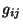 são as componentes de um tensor de segunda
ordem. Este tensor, um dos mais importantes, é
denominado tensor métrico.
são as componentes de um tensor de segunda
ordem. Este tensor, um dos mais importantes, é
denominado tensor métrico.



Next: Eixos não ortogonais
Up: Mudanças de base
Previous: Transformações das componentes de
Henrique Fleming
2002-04-15