


Next: O momento de inércia
Up: Mudanças de base
Previous: Mudanças de base
Seja
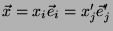 um vetor qualquer. Temos
um vetor qualquer. Temos
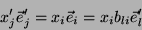 |
(10) |
ou, o que é o mesmo,
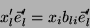 |
(11) |
de onde segue que
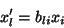 |
(12) |
Inversamente,
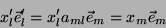 |
(13) |
de onde sai que
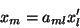 |
(14) |
ou, resumindo,
Note-se que
Diz-se que a combinação das componentes de um vetor dada por 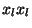 é um invariante.
Considerando
é um invariante.
Considerando 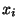 e
e 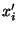 como coordenadas de um mesmo ponto,
temos a função
como coordenadas de um mesmo ponto,
temos a função 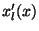 , e, então,
, e, então,
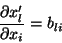 |
(17) |
e
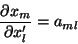 |
(18) |
Desta forma,
No que se segue, vamos definir um vetor através das Eqs.(
19), ou seja, através das propriedades de transformação
de suas componentes. Isto se faz mais ou menos assim: seja 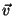 um
vetor, isto é, um conjunto de pares
um
vetor, isto é, um conjunto de pares 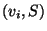 , onde
, onde 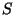 é uma base
e
é uma base
e
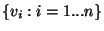 números ditos componentes nessa base, relacionados
de uma base para outra, pelas Eq.(19). Para
mostrar que o conjunto dos vetores assim definidos forma um espaço vetorial,
definamos, dados
números ditos componentes nessa base, relacionados
de uma base para outra, pelas Eq.(19). Para
mostrar que o conjunto dos vetores assim definidos forma um espaço vetorial,
definamos, dados 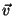 e um número
e um número 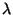 , o vetor
, o vetor
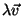 . É o vetor de componentes
. É o vetor de componentes 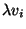 . Dados
dois vetores,
. Dados
dois vetores, 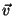 e
e 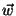 , definamos o vetor
, definamos o vetor
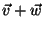 como aquele cujas componentes são
como aquele cujas componentes são 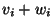 . É facil mostrar que,
nessas condições , o conjunto dos vetores forma um espaço vetorial.
Nosso próximo passo é mostrar que existem quantidades mais
complexas que os vetores e que têm interesse físico.
. É facil mostrar que,
nessas condições , o conjunto dos vetores forma um espaço vetorial.
Nosso próximo passo é mostrar que existem quantidades mais
complexas que os vetores e que têm interesse físico.



Next: O momento de inércia
Up: Mudanças de base
Previous: Mudanças de base
Henrique Fleming
2002-04-15