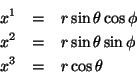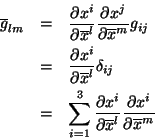Next: Um exemplo importante
Up: Métrica no espaço
Previous: Métrica no espaço
No caso do espaço euclideano 3-dimensional com coordenadas
cartesianas ortogonais,
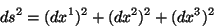 |
(86) |
isto é, em coordenadas cartesianas
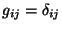 .
Descrevendo o mesmo espaço com coordenadas esféricas
.
Descrevendo o mesmo espaço com coordenadas esféricas
e chamando
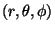 , nessa ordem, de
, nessa ordem, de
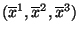 , temos, como
, temos, como 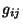 é um
tensor,
é um
tensor,
Obtivemos, então, uma fórmula para calcular o tensor métrico
para quaisquer corrdenadas, a partir de seus valores em coordenadas
cartesianas. Para coordenadas esféricas,
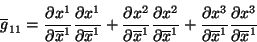 |
(87) |
ou seja,
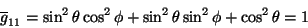 |
(88) |
Por um cálculo análogo chega-se a
Então o elemento de linha em coordenadas esféricas é
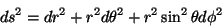 |
(91) |



Next: Um exemplo importante
Up: Métrica no espaço
Previous: Métrica no espaço
Henrique Fleming
2002-04-15