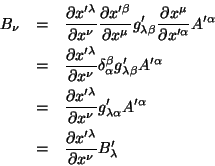Next: Mais sobre o tensor
Up: Conceito geral de tensor
Previous: ``Macetes''
Seja 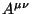 um conjunto de números tais que
um conjunto de números tais que
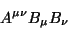 |
(77) |
seja um invariante, para vetores covariantes 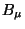 arbitrários. Então
arbitrários. Então
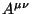 é um tensor duas vezes contravariante. De fato, sejam
é um tensor duas vezes contravariante. De fato, sejam
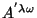 as componentes de
as componentes de 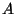 na nova base. Então, como a expressão
(77) é invariante, temos
na nova base. Então, como a expressão
(77) é invariante, temos
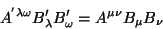 |
(78) |
Mas
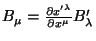 , com
uma expressão análoga para
, com
uma expressão análoga para 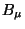 . Segue que
. Segue que
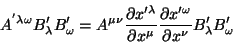 |
(79) |
logo,
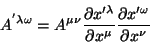 |
(80) |
e isto prova a nossa tese. Analogamente, se 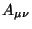 são tais
que, para vetores
são tais
que, para vetores 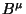 arbitrários,
arbitrários,
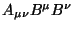 é invariante, então
é invariante, então 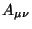 é um tensor duas vezes
contravariante.
é um tensor duas vezes
contravariante.
Corolário:
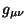 é um tensor duas vezes covariante.
De fato,
é um tensor duas vezes covariante.
De fato,
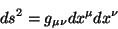 |
(81) |
é um invariante para qualquer 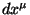 .
O tensor
.
O tensor 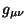 é de grande importância, pelo que se segue.
Seja
é de grande importância, pelo que se segue.
Seja 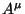 um vetor contravariante, e considere a expressão
um vetor contravariante, e considere a expressão
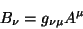 |
(82) |
Como
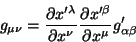 |
(83) |
e
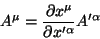 |
(84) |
tem-se
isto é, 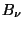 é um vetor covariante, que depende só de
é um vetor covariante, que depende só de 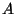 e
do tensor métrico. Por isso, adota-se a convenção de usar para este
particular
e
do tensor métrico. Por isso, adota-se a convenção de usar para este
particular 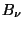 a notação
a notação 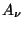 . Conclusão: usando a
métrica, associa-se a cada vetor contravariante
. Conclusão: usando a
métrica, associa-se a cada vetor contravariante 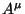 um único vetor
covariante
um único vetor
covariante 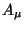 . Deixa-se, então, quando há uma métrica, de
falar em ``vetor contravariante'' ou ``vetor covariante'', para falar
simplesmente de vetor, que tem componentes covariantes e
componentes contravariantes.
A operação
. Deixa-se, então, quando há uma métrica, de
falar em ``vetor contravariante'' ou ``vetor covariante'', para falar
simplesmente de vetor, que tem componentes covariantes e
componentes contravariantes.
A operação
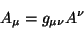 |
(85) |
``baixa'' o índice de 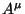 .
.
Teorema: uma equação 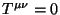 , onde as componentes são
em relação a um base
, onde as componentes são
em relação a um base 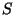 , implica que, em qualquer outra base
, implica que, em qualquer outra base
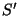 , se tenha
, se tenha
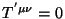 . Ou seja, o tensor que tem todas
as componentes nulas em uma base, as tem nulas em todas as bases.
A demonstração é trivial, a partir das fórmulas de transformação
das componentes.
. Ou seja, o tensor que tem todas
as componentes nulas em uma base, as tem nulas em todas as bases.
A demonstração é trivial, a partir das fórmulas de transformação
das componentes.
Subsections



Next: Mais sobre o tensor
Up: Conceito geral de tensor
Previous: ``Macetes''
Henrique Fleming
2002-04-15