


Next: Transformações de Lorentz
Up: Métrica no espaço
Previous: Mais sobre o tensor
Consideremos as transformações lineares homogêneas que mantêm
invariante a distância euclideana
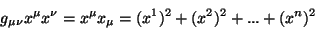 |
(92) |
A primeira coisa a notar é que
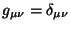 .
Em conseqüência ,
.
Em conseqüência ,
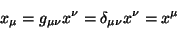 |
(93) |
ou seja, as componentes contravariantes e as covariantes
coincidem. Restringindo-nos apenas a bases ortonormais, temos
ainda que
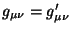 , ou seja, as componentes
do tensor métrico são sempre as mesmas, em qualquer base
(ortonormal). Por outro lado, a fórmula geral de transformação
dessas componentes é:
, ou seja, as componentes
do tensor métrico são sempre as mesmas, em qualquer base
(ortonormal). Por outro lado, a fórmula geral de transformação
dessas componentes é:
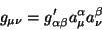 |
(94) |
onde os
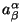 são os coeficientes de
transformação das coordenadas de um sistema para o outro,
isto é:
são os coeficientes de
transformação das coordenadas de um sistema para o outro,
isto é:
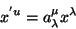 |
(95) |
A Eq.(94) pode então ser escrita
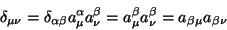 |
(96) |
ou ainda
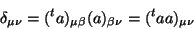 |
(97) |
que quer dizer que
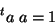 |
(98) |
como matrizes. A matriz 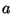 é, então, ortogonal, resultado
que já havíamos obtido anteriormente, de outra forma.
é, então, ortogonal, resultado
que já havíamos obtido anteriormente, de outra forma.



Next: Transformações de Lorentz
Up: Métrica no espaço
Previous: Mais sobre o tensor
Henrique Fleming
2002-04-15