


Next: O tensor eletromagnético
Up: O eletromagnetismo relativista
Previous: A equação da continuidade
Considere agora a quantidade
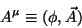 |
(132) |
onde 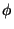 é o potencial escalar e
é o potencial escalar e 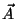 é o potencial vetor.
Usando a definição dada acima de
é o potencial vetor.
Usando a definição dada acima de 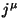 podemos escrever as equações
para os potenciais assim;
podemos escrever as equações
para os potenciais assim;
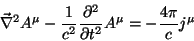 |
(133) |
Mas o operador diferencial
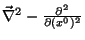 é um invariante, pois
é um invariante, pois
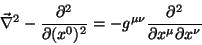 |
(134) |
onde usamos, pela primeira vez, o tensor 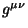 , que é o próprio
tensor métrico, mas expresso em termos de suas componentes contravariantes.
É costume usar-se a notação
, que é o próprio
tensor métrico, mas expresso em termos de suas componentes contravariantes.
É costume usar-se a notação 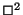 para o operador
para o operador
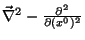 , que tem também um nome:
D'Alembertiano. Então a equação para os potenciais fica
, que tem também um nome:
D'Alembertiano. Então a equação para os potenciais fica
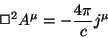 |
(135) |
Mas 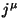 é um 4-vetor, logo
é um 4-vetor, logo
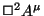 também é. Como,
além disso,
também é. Como,
além disso, 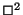 é um invariante, segue de (135) que
é um invariante, segue de (135) que
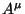 também é um 4-vetor.
Há ainda uma coisa a ser demonstrada: a eq.(135) para os potenciais
só é equivalente às equações de Maxwell se a condição de Lorenz,
também é um 4-vetor.
Há ainda uma coisa a ser demonstrada: a eq.(135) para os potenciais
só é equivalente às equações de Maxwell se a condição de Lorenz,
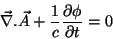 |
(136) |
for satisfeita. Como a eq.(135) precisa ser verdadeira em todos
os referenciais, por ser um escalar igualado a zero, é preciso mostrar que
também a condição de Lorenz é um invariante. Felizmente isto é muito
facil:
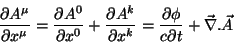 |
(137) |
Logo, a condição de Lorenz é invariante, dada por
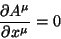 |
(138) |



Next: O tensor eletromagnético
Up: O eletromagnetismo relativista
Previous: A equação da continuidade
Henrique Fleming
2002-04-15