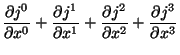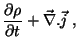Next: O 4-vetor potencial
Up: O eletromagnetismo relativista
Previous: O eletromagnetismo relativista
A equação da continuidade é nossa velha conhecida. Na linguagem tradicional
ela se escreve
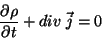 |
(117) |
Vamos introduzir a seguinte quantidade, de 4 componentes:
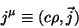 |
(118) |
que significa o seguinte: as componentes de 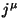 são
são 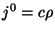 ,
,
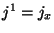 ,
, 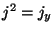 e
e 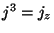 . Com essa notação , a equação da
continuidade pode ser expressa de uma forma compacta:
. Com essa notação , a equação da
continuidade pode ser expressa de uma forma compacta:
logo, a equação da continuidade pode ser escrita
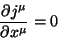 |
(121) |
Mas há muito mais do que comodismo nisso. O próximo passo é
o seguinte postulado: 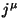 é um 4-vetor. No momento em que
digo isto, a Eq.(121) adquire um significado muito maior, pois,
se
é um 4-vetor. No momento em que
digo isto, a Eq.(121) adquire um significado muito maior, pois,
se 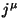 é um 4-vetor,
é um 4-vetor,
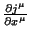 é um invariante (ou escalar), e a equação (121) diz que
um escalar é igual a zero num sistema de referência. Logo, é
igual a zero em qualquer sistema de referência (inercial, bem entendido).
Ou seja, supor que
é um invariante (ou escalar), e a equação (121) diz que
um escalar é igual a zero num sistema de referência. Logo, é
igual a zero em qualquer sistema de referência (inercial, bem entendido).
Ou seja, supor que 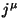 é um 4-vetor é um grande passo, cheio de
conseqüências. Por que
é um 4-vetor é um grande passo, cheio de
conseqüências. Por que 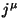 é um 4-vetor? É um palpite (embora tenha
o nome pomposo de postulado). Vamos ver se dá certo. Se todas as
consequências desse palpite forem verdades da natureza, o palpite
está apoiado pela experiência. É assim que se faz ciência5.
Suponhamos que
é um 4-vetor? É um palpite (embora tenha
o nome pomposo de postulado). Vamos ver se dá certo. Se todas as
consequências desse palpite forem verdades da natureza, o palpite
está apoiado pela experiência. É assim que se faz ciência5.
Suponhamos que 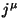 seja, mesmo, um 4-vetor. Então,
seja, mesmo, um 4-vetor. Então,
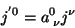 |
(122) |
Para a transformação especial de Lorentz, teremos
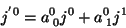 |
(123) |
Tomemos aquele particular 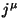 , em
, em 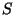 , que tem a forma
, que tem a forma
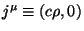 , ou seja, uma carga em repouso em
, ou seja, uma carga em repouso em 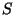 . Então,
no sistema
. Então,
no sistema 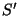 ,
,
Temos ainda a componente 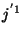
O resultado faz sentido, pois o observador ligado a 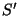 vê uma carga se movendo
com velocidade
vê uma carga se movendo
com velocidade 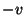 e, pelo cálculo anterior, com uma densidade de carga
e, pelo cálculo anterior, com uma densidade de carga 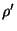 .
Uma conseqüência importante é que a carga é um invariante. De fato, pela
contração de Lorentz sabemos que um volume
.
Uma conseqüência importante é que a carga é um invariante. De fato, pela
contração de Lorentz sabemos que um volume 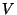 para o observador em
para o observador em 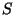 é
visto pelo observador em
é
visto pelo observador em 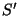 como
como
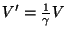 . Então, temos
. Então, temos
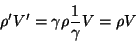 |
(131) |
e a carga é um invariante. Um bom teste experimental da invariância da carga
é o seguinte: considere um fio comum de instalação elétrica. Ele é neutro,
as cargas negativas exatamente compensando as cargas positivas. Aqueço
o fio. À nova temperatura, os elétrons terão ganho muito mais velocidade do
que os íons positivos (pois a energia cinética média é igual para os dois, e as
massas são muito diferentes). No entanto, o fio continua neutro, mostrando que
a igualdade das cargas continua a ser verificada.



Next: O 4-vetor potencial
Up: O eletromagnetismo relativista
Previous: O eletromagnetismo relativista
Henrique Fleming
2002-04-15