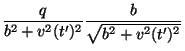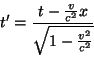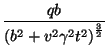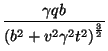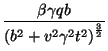Next: Campo de um fio
Up: Aplicações
Previous: Aplicações
Uma partícula se move com velocidade constante 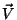 . Pergunta-se quais os
campos criados por ela.
Vamos resolver este problema por meio de uma trnsformação de Lorentz adequada.
Suponhamos que a partícula esteja em repouso no sistema de referência
. Pergunta-se quais os
campos criados por ela.
Vamos resolver este problema por meio de uma trnsformação de Lorentz adequada.
Suponhamos que a partícula esteja em repouso no sistema de referência 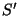 .
O observador em
.
O observador em 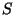 vai, então, vê-la nas condições do problema. No sistema
vai, então, vê-la nas condições do problema. No sistema
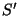 , o campo da partícula é o campo coulombiano. No ponto
, o campo da partícula é o campo coulombiano. No ponto 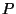 (veja a
figura)
o campo é
(veja a
figura)
o campo é
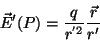 |
(171) |
com
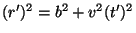 , e suas componentes nas direções
, e suas componentes nas direções 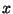 e
e 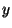 .
Temos
.
Temos
Note-se agora que
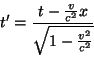 |
(175) |
e, como o ponto 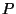 está em
está em 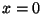 ,
,
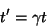 |
(176) |
Nas coordenadas do observador em 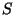 , então,
, então,
Usando agora as fórmulas de transformação (Eq.164 e seguintes),
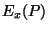 |
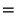 |
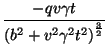 |
(180) |
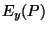 |
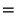 |
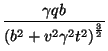 |
(181) |
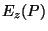 |
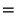 |
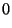 |
(182) |
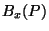 |
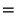 |
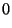 |
(183) |
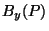 |
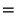 |
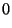 |
(184) |
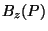 |
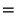 |
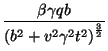 |
(185) |
Para entender a aparência do campo elétrico, note-se que
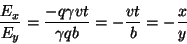 |
(186) |
isto é, o campo 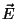 , como o
, como o 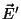 , é também radial. Como
, é também radial. Como
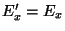 e
e
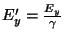 , o campo transversal é mais forte
do que o longitudinal, em relação ao campo
, o campo transversal é mais forte
do que o longitudinal, em relação ao campo 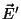 .
.



Next: Campo de um fio
Up: Aplicações
Previous: Aplicações
Henrique Fleming
2002-04-15
{$q$}
\end{pspicture}](img366.png)