


Next: Bibliography
Up: Aplicações
Previous: Partícula com velocidade constante
Para simplificar suponhamos que a corrente seja produzida por um feixe
de elétrons com velocidade constante (sem a contrapartida de íons
positivos, como num fio). Isto será simbolizado por um fio infinito
(que poderia ser um tubo oco, dentro do qual estariam passando
os elétrons).
Um fio infinito ao longo do eixo 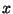 .
.
O sistema 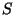 , que possui velocidade
, que possui velocidade 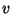 em relação ao sistema
em relação ao sistema 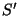 ,
enxerga os elétrons parados (
,
enxerga os elétrons parados (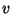 é também a velocidade dos
elétrons!). Neste sistema (
é também a velocidade dos
elétrons!). Neste sistema (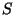 ), então, o campo magnético é nulo,
e o campo elétrico é perpendicular ao fio, radial e de módulo
), então, o campo magnético é nulo,
e o campo elétrico é perpendicular ao fio, radial e de módulo
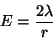 |
(187) |
onde 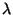 é a densidade linear de carga. Este resultado pode
ser facilmente obtido usando-se o teorema de Gauss, por exemplo. No ponto
é a densidade linear de carga. Este resultado pode
ser facilmente obtido usando-se o teorema de Gauss, por exemplo. No ponto
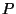 (veja a figura), temos
(veja a figura), temos
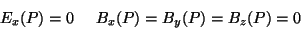 |
(188) |
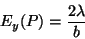 |
(189) |
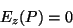 |
(190) |
Usando as fórmulas de transformação obtemos
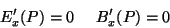 |
(191) |
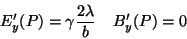 |
(192) |
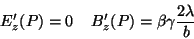 |
(193) |
Em suma, o campo magnético é
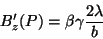 |
(194) |
Se um observador ``em repouso'' observa uma carga por unidade de comprimento
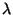 e uma corrente zero, quais serão a densidade de carga e a
corrente observadas por um observador de velocidade
e uma corrente zero, quais serão a densidade de carga e a
corrente observadas por um observador de velocidade 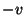 ? Suponhamos
que o fio tenha uma secção reta de área
? Suponhamos
que o fio tenha uma secção reta de área 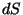 . Tomando um comprimento
. Tomando um comprimento
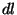 do fio, temos um volume
do fio, temos um volume 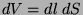 . A carga neste volume é
. A carga neste volume é 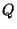 .
.
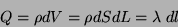 |
(195) |
Logo,
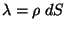 . Então
. Então 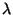 se transforma como
se transforma como
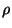 , pois
, pois 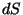 , transversal à velocidade, é invariante. Mas,
como
, transversal à velocidade, é invariante. Mas,
como 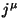 é um 4-vetor,
é um 4-vetor,
e
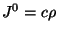 (e, neste caso,
(e, neste caso, 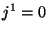 ). Segue então que
). Segue então que
A corrente observada por 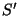 é
é
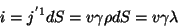 |
(200) |
Levando este resultado à Eq.(194),
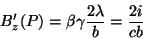 |
(201) |
que é o resultado que obtivemos antes pela lei circuital de
Ampère. Pode-se ainda calcular o campo elétrico em 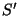 , ou seja,
o campo elétrico de um fio infinito por onde passa uma corrente
, ou seja,
o campo elétrico de um fio infinito por onde passa uma corrente 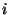 .
Este campo é, como vimos,
.
Este campo é, como vimos,
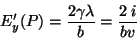 |
(202) |
que é um resultado bastante interessante, pois não depende só da
corrente, mas também da velocidade. Assim, medindo-se simultaneamente
os dois campos, pode-se determinar a corrente (através de 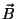 )
e depois a velocidade das partículas, através de
)
e depois a velocidade das partículas, através de 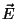 .
.



Next: Bibliography
Up: Aplicações
Previous: Partícula com velocidade constante
Henrique Fleming
2002-04-15
(10,3)
\psline{->}(1,3...
...uput[0](1,4){$b$}
\uput[0](5,5.5){$S$}
\uput[0](9.5,2.8){$x$}
\end{pspicture}](img389.png)
(10,3)
\psline{->}(1,3...
...uput[0](1,4){$b$}
\uput[0](5,5.5){$S$}
\uput[0](9.5,2.8){$x$}
\end{pspicture}](img389.png)