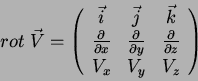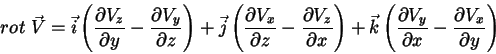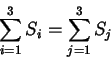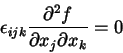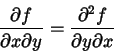Next: Aplicações ``peso-pesado''
Up: Teorema importantíssimo
Previous: Teorema importantíssimo
A primeira aplicação do teorema importantíssimo
(eq.(17)) é o cálculo do duplo produto vetorial,
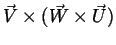 .
Temos:
.
Temos:
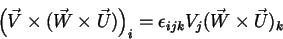 |
(18) |
Por outro lado,
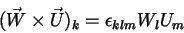 |
(19) |
de modo que
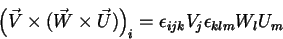 |
(20) |
Nesta última equação temos a combinação
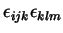 , que é a mesma coisa que
, que é a mesma coisa que
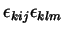 . Pelo teorema importantíssimo,
. Pelo teorema importantíssimo,
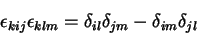 |
(21) |
Levando este resultado à eq.(20), temos
ou seja, finalmente,
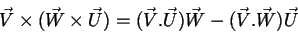 |
(23) |
Para a segunda aplicação vamos introduzir o ``vetor''
 , cujas componentes são dadas por
, cujas componentes são dadas por
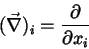 |
(24) |
onde 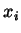 representa, claramente, a
representa, claramente, a 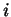 -ésima coordenada cartesiana
-ésima coordenada cartesiana
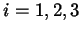 . Usaremos também uma abreviação mais drástica:
. Usaremos também uma abreviação mais drástica:
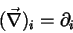 |
(25) |
Com isto podemos introduzir o divergente de um campo vetorial. Sejam
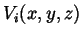 as componentes cartesianas de um campo vetorial. O campo
escalar
as componentes cartesianas de um campo vetorial. O campo
escalar 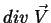 é descrito por
é descrito por
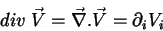 |
(26) |
Um desafio mais interessante é o tratamento do operador 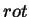 . O
rotacional do campo vetorial
. O
rotacional do campo vetorial 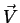 é em geral apresentado em
termos de suas coordenadas cartesianas, dadas pelo determinante
simbólico:
é em geral apresentado em
termos de suas coordenadas cartesianas, dadas pelo determinante
simbólico:
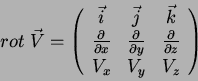 |
(27) |
que significa
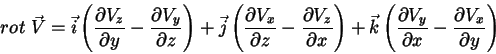 |
(28) |
Para a nossa notação é útil lembrar que
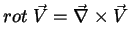 . Por isso,
. Por isso,
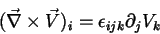 |
(29) |
Como mais uma aplicação simples, vamos mostrar que
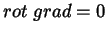 .
.
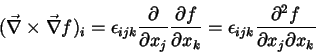 |
(30) |
Para mostrar que isto é zero, vamos recorrer a outro resultado
importante. Seja 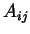 tal que
tal que
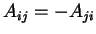 , e
, e
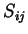 tal que
tal que 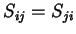 . Dizemos que
. Dizemos que 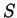 é simétrica, e
que
é simétrica, e
que 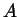 é antissimétrica. Vamos mostrar que
é antissimétrica. Vamos mostrar que
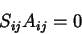 |
(31) |
(Note que um caso particular desta relação é que
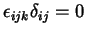 , pois
, pois
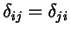 enquanto
enquanto
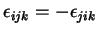 ).
A prova é esta:
).
A prova é esta:
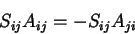 |
(32) |
pela antissimetria de 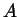 . Agora, mudamos os nomes dos índices:
aquele que era denotado por
. Agora, mudamos os nomes dos índices:
aquele que era denotado por 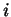 passa a ser denotado por
passa a ser denotado por 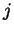 , e
vice-versa. A expressão anterior então fica, repetindo-a desde o
começo:
, e
vice-versa. A expressão anterior então fica, repetindo-a desde o
começo:
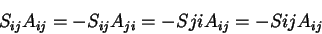 |
(33) |
onde, na última igualdade, usamos a simetria de 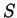 . Comparando os
dois extremos, vemos que temos uma expressão
. Comparando os
dois extremos, vemos que temos uma expressão 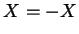 , cuja única
solução é 0. Logo,
, cuja única
solução é 0. Logo,
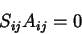 |
(34) |
Um ponto que em geral causa perplexidade é a ``mudança de nome''
dos índices. Isto é uma coisa muito simples, se se restaura,
por um momento o símbolo de somatório:
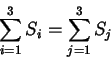 |
(35) |
ou seja, a letra que designa a soma é arbitrária. Podemos
trocá-la à vontade. Por isso,
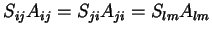 .
.
Voltando à eq.(30), temos
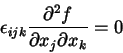 |
(36) |
pois se aprende no Cálculo Diferencial e Integral que a derivada
mista não depende da ordem de derivação, ou seja, por exemplo,
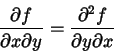 |
(37) |
Logo, a eq.(30) nos diz que
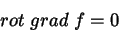 |
(38) |
qualquer que seja 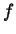 .
.



Next: Aplicações ``peso-pesado''
Up: Teorema importantíssimo
Previous: Teorema importantíssimo
Henrique Fleming
2001-12-18
![]() , cujas componentes são dadas por
, cujas componentes são dadas por