


Next: Comentários
Up: Cálculo Vetorial Prático
Previous: Aplicações
Aqui veremos resultados que são difíceis, ou muito trabalhosos,
de obter por outros métodos. Em primeiro lugar, vamos mostrar (como
aquecimento) que 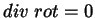 .
.
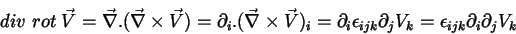 |
(39) |
Ora,
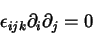 |
(40) |
pois
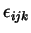 é antissimétrico pela troca de índices
é antissimétrico pela troca de índices
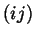 , e
, e
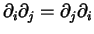 . Segue que
. Segue que
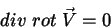 |
(41) |
qualquer que seja 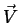 .
.
Seja 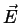 um campo vetorial. Por exemplo, o campo elétrico. Na
teoria de Maxwell precisamos calcular
um campo vetorial. Por exemplo, o campo elétrico. Na
teoria de Maxwell precisamos calcular
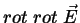 . Com o nosso
método, isso é simples:
. Com o nosso
método, isso é simples:
Resta interpretar o resultado. A última linha pode ser escrita:
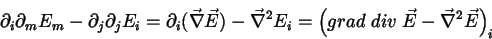 |
(43) |
Logo,
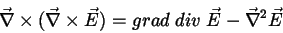 |
(44) |
Outra relação de grande importância na eletrodinâmica
envolve o cálculo de
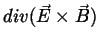 .
.
Finalmente, vamos ao nosso tour de force: calcular
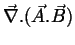 .
.
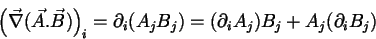 |
(46) |
Temos, preliminarmente, que
de maneira que, também preliminarmente,
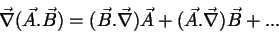 |
(49) |
Para calcular os termos adicionais, notemos que
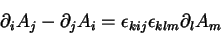 |
(50) |
como o leitor, a esta altura, poderá facilmente verificar. Logo,
Analogamente,
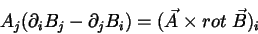 |
(52) |
Juntando estes termos à eq.(49), temos
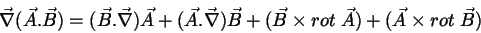 |
(53) |



Next: Comentários
Up: Cálculo Vetorial Prático
Previous: Aplicações
Henrique Fleming
2001-12-18
![]() um campo vetorial. Por exemplo, o campo elétrico. Na
teoria de Maxwell precisamos calcular
um campo vetorial. Por exemplo, o campo elétrico. Na
teoria de Maxwell precisamos calcular
![]() . Com o nosso
método, isso é simples:
. Com o nosso
método, isso é simples:
![]() .
.
![]() .
.